``#### 回歸和分類

數據集：圖片，視頻，表格

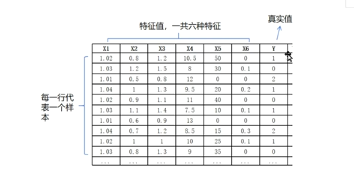
特徵值可以理解爲屬性

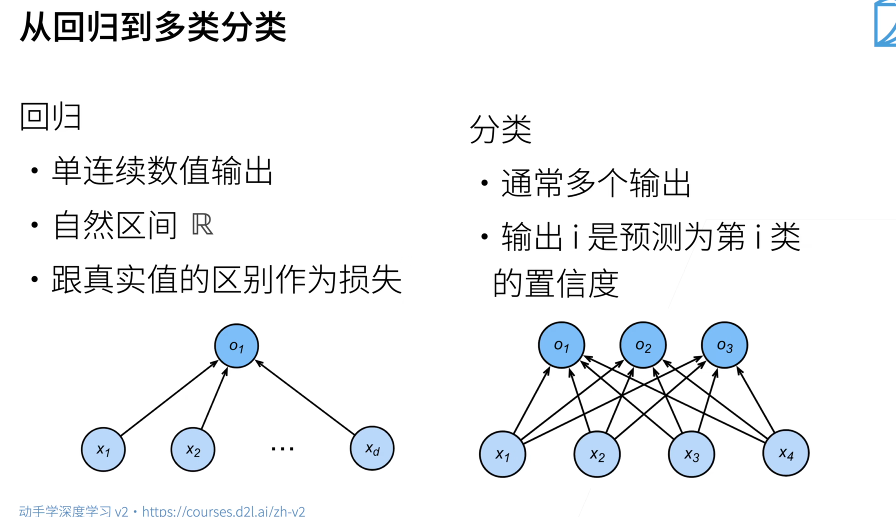
從回歸到分類

對於分類來說，不太關心實際的數值如何，而是使正確類別的置信度最大即可 也就是讓某一類 Oy遠大於其他類

極大似然估計

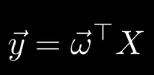
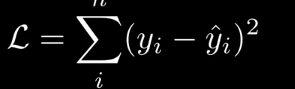
在正態分佈中

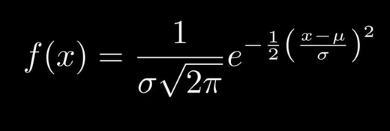
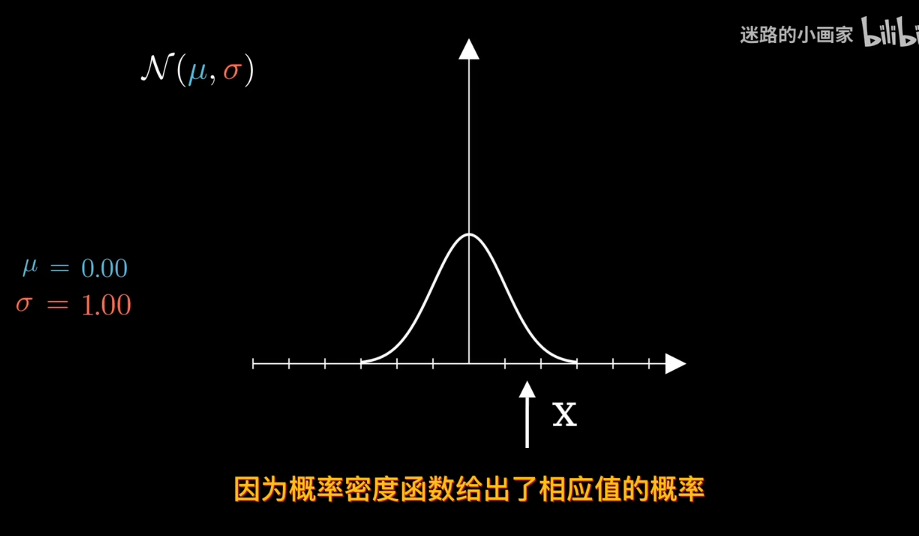
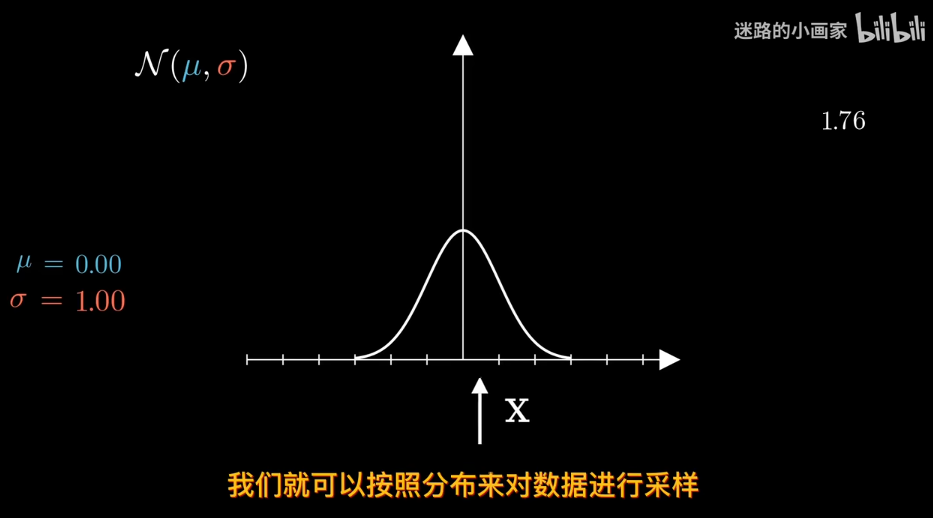
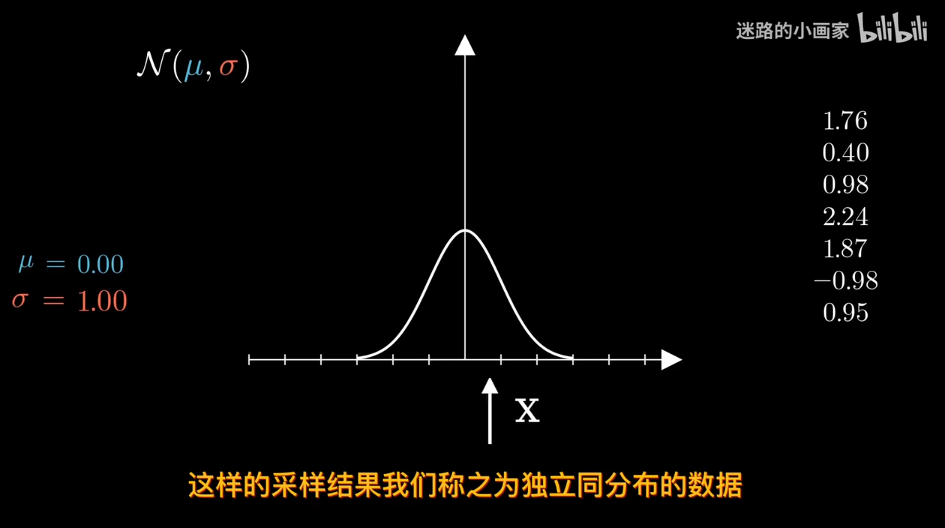
給定數據確定分佈？

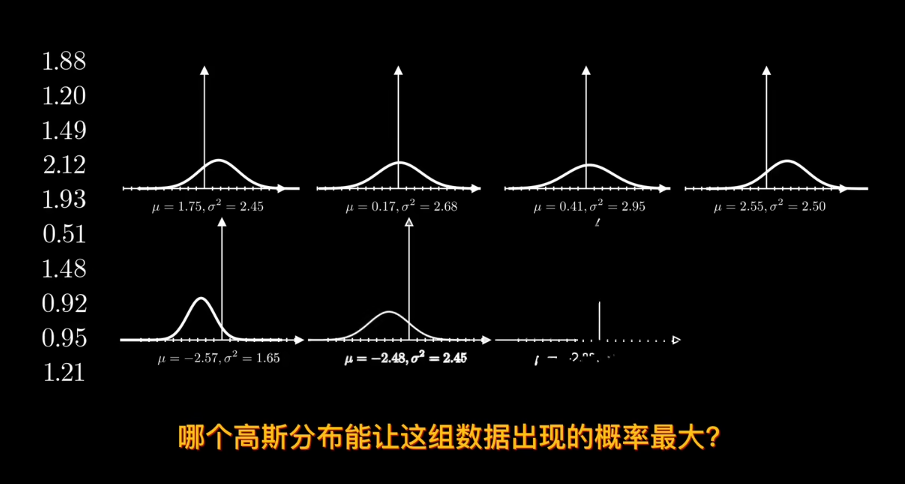
知道概率分佈求概率叫估計 知道概率求分佈叫似然

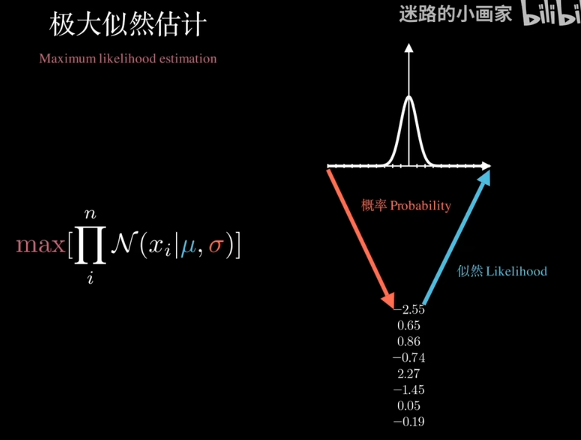
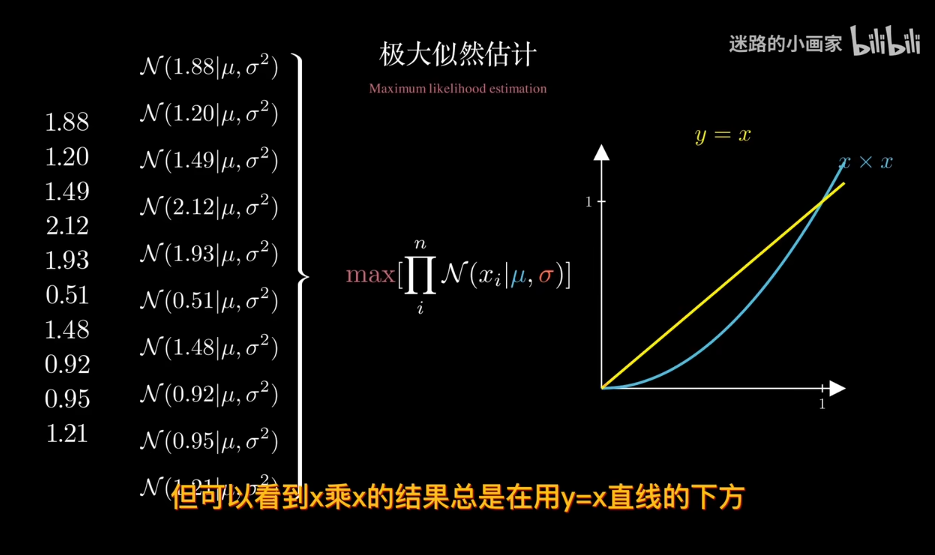
結果會非常小，甚至爲0

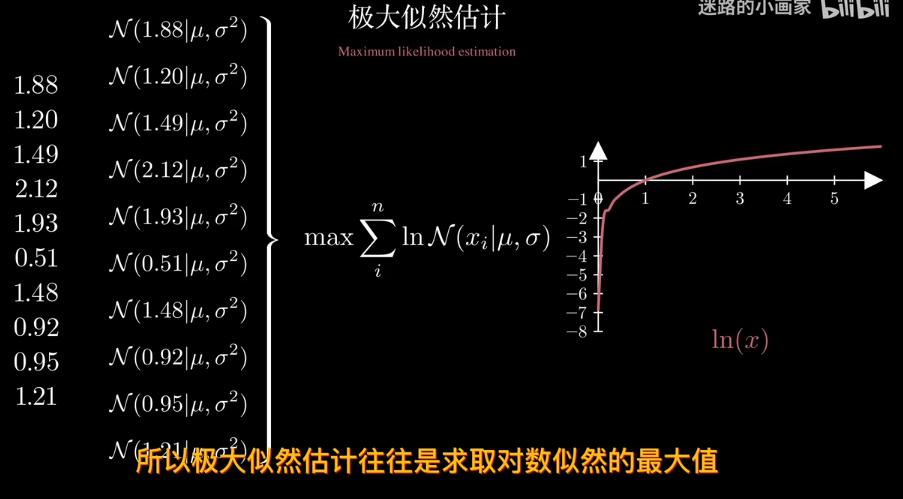
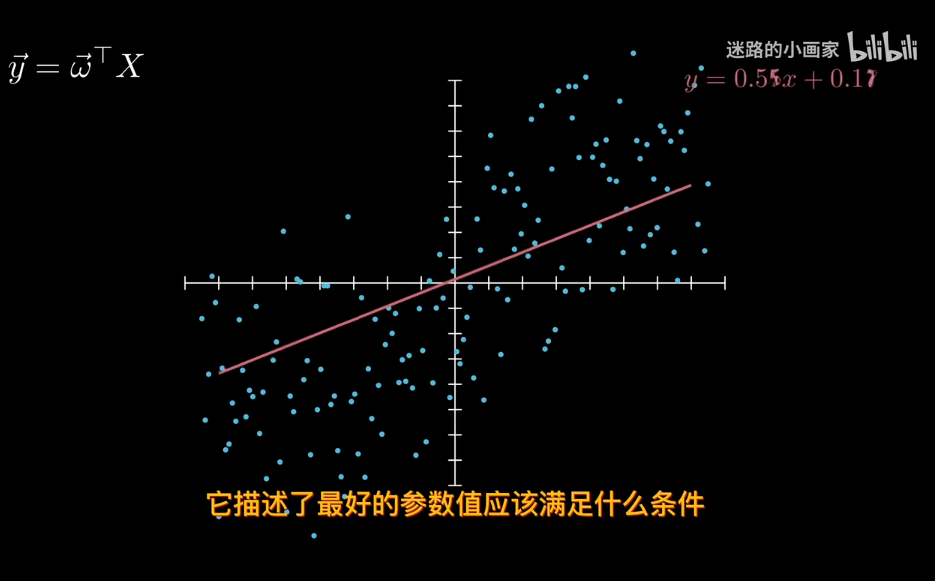
回到線性回歸

x已知下，y是不確定的.

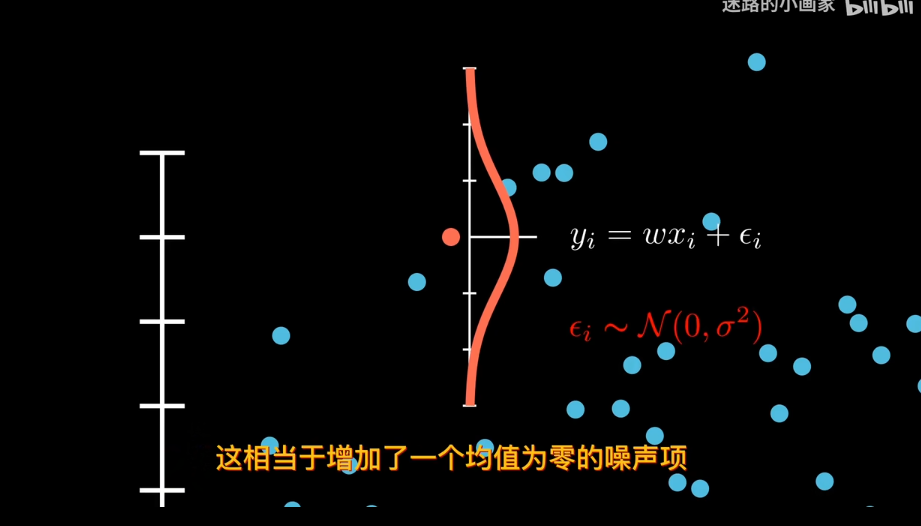
均值為 0 的假設還意味著噪聲是「無偏」的，即它不會系統性地高估或低估目標值，而是在 f(x)附近隨機波動。

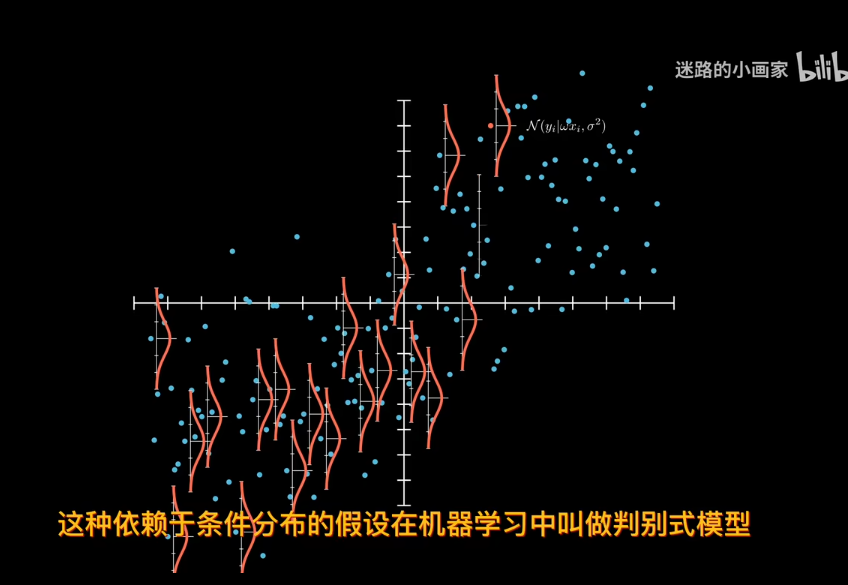
對分佈化簡，剔除與模型無關的噪聲sigma

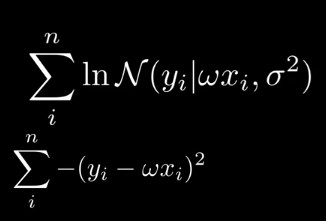
現在求w的最可能值。對於同分佈數據點，求極大似然估計。

‘

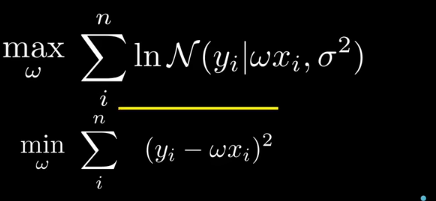線性回歸中，目標值y假設是由高斯分佈採樣而來，也就是說值域爲實數

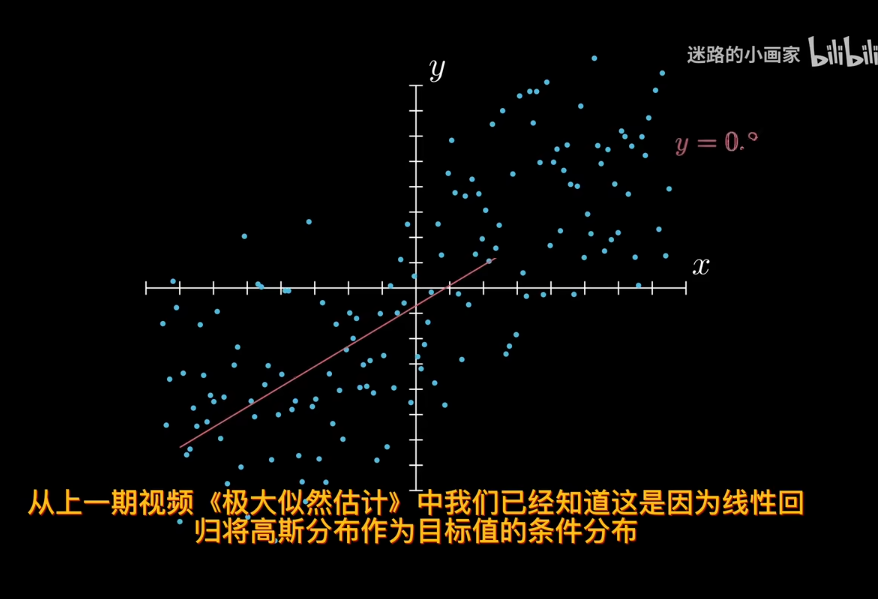
但二分類問題，目標值只能取0或者1，也就是值域的範圍發生了變化

那麼引入參數來表是線性模型輸出結果

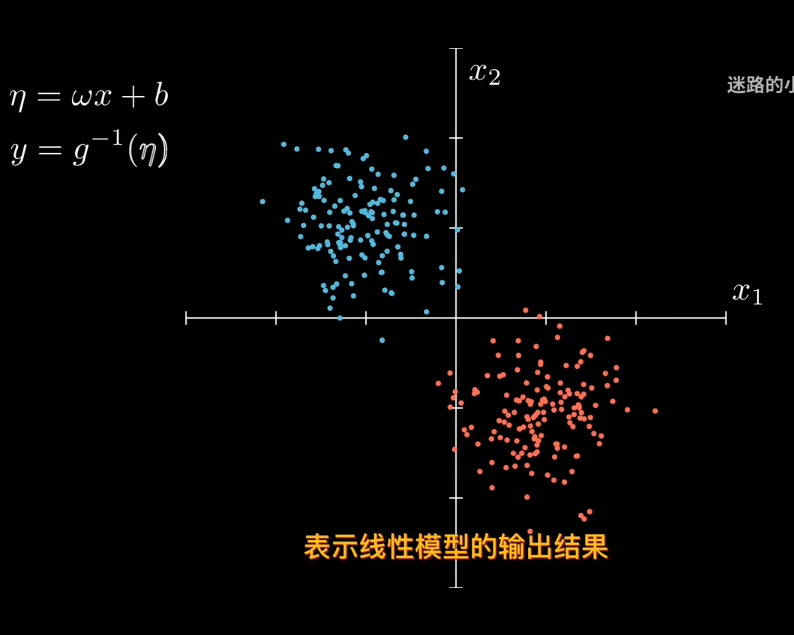
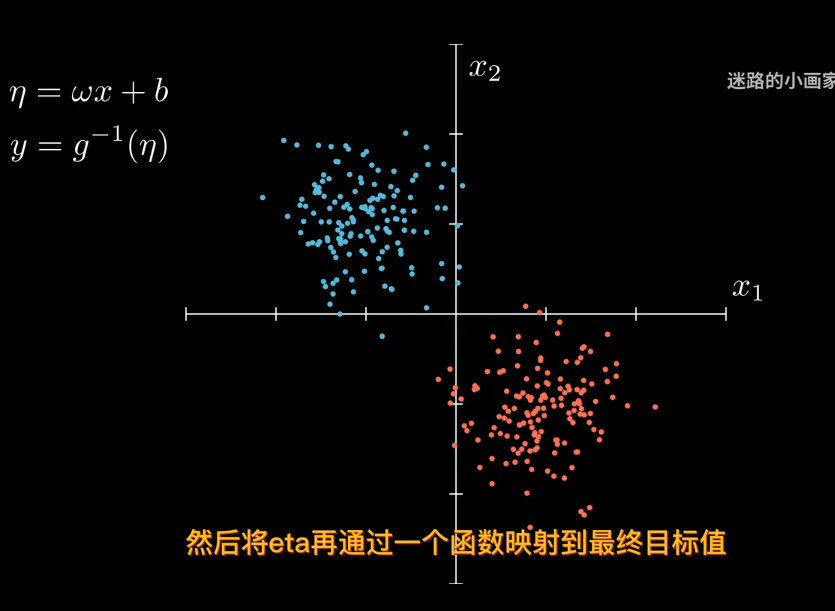
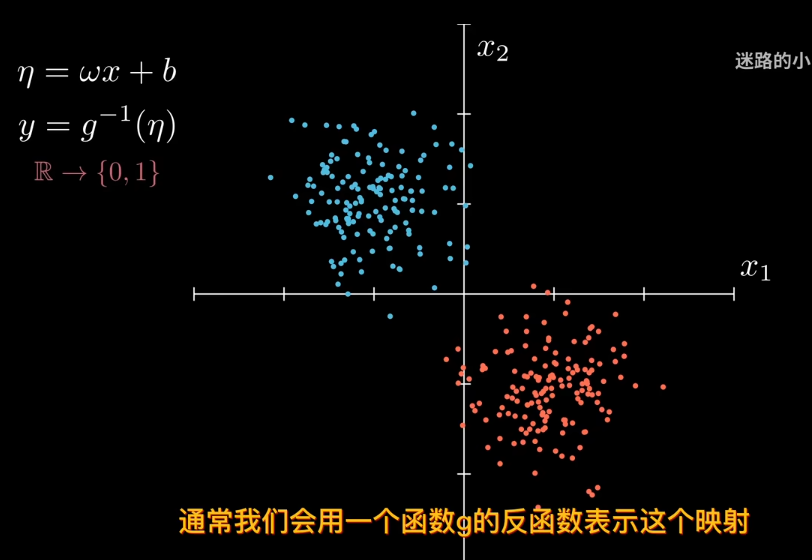
比如sigmod函數

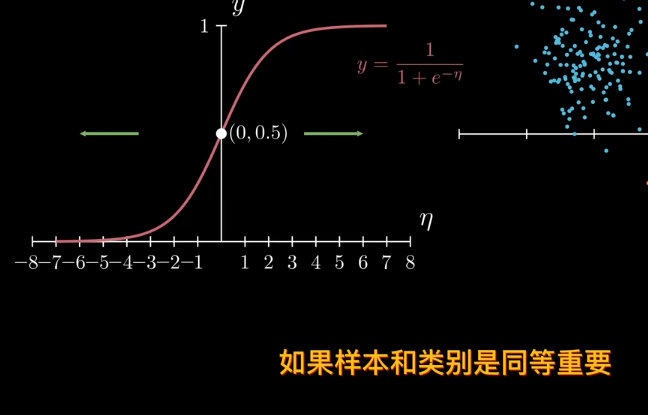
但sigmod函數是中心對稱，也就是說樣本和類別同等重要，不存在某一種類別對目標值的貢獻低

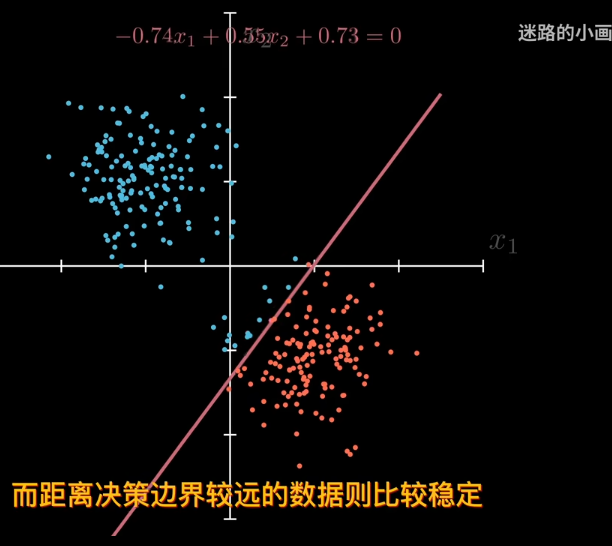
因爲sigmod單調，可以賦予概率。離決策邊界越遠屬於該類概率越大

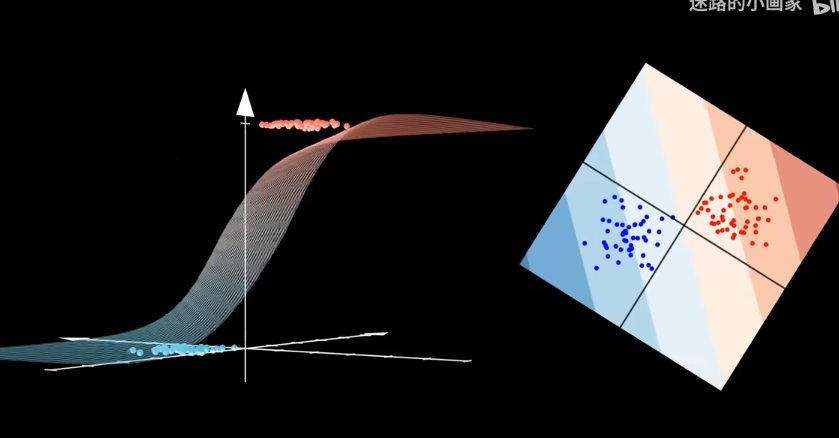
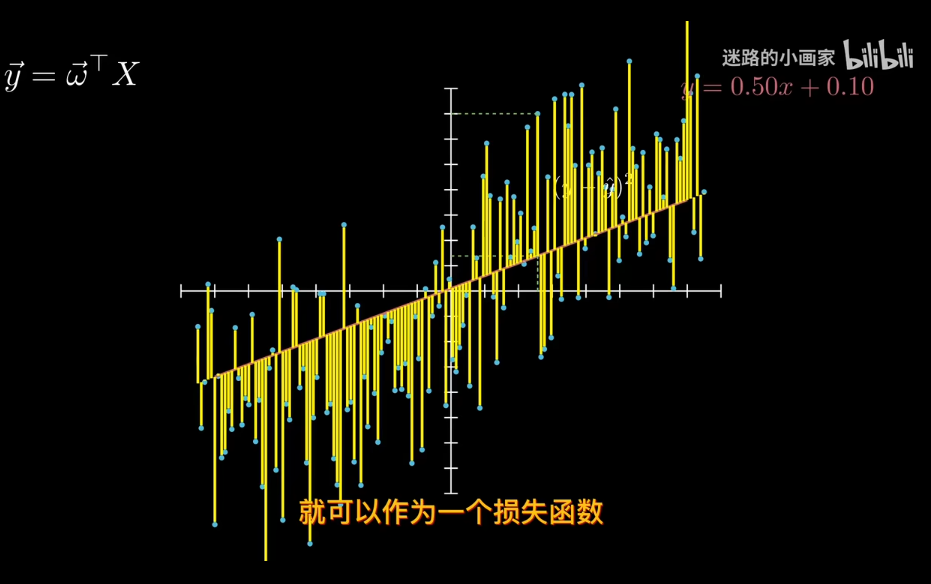
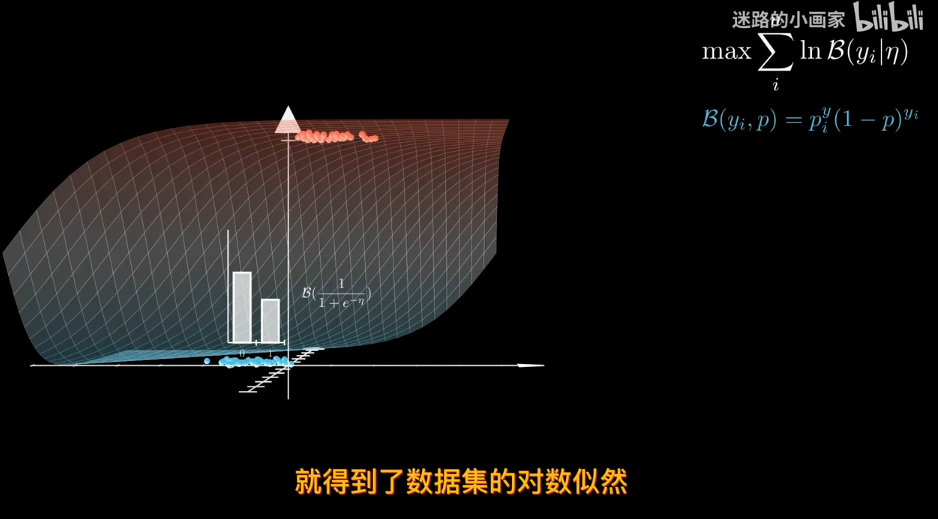
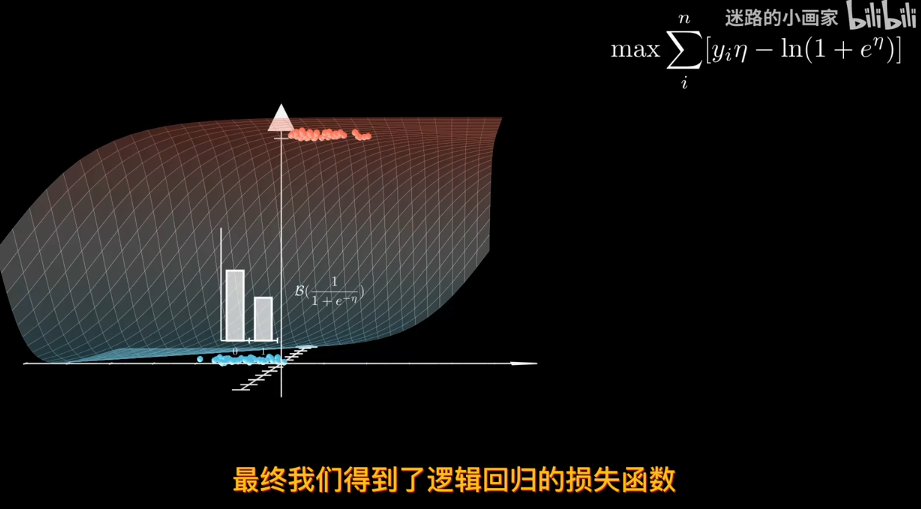
那麼爲了找出最合適的決策邊界，需要定義一個損失函數 比如利用極大似然估計

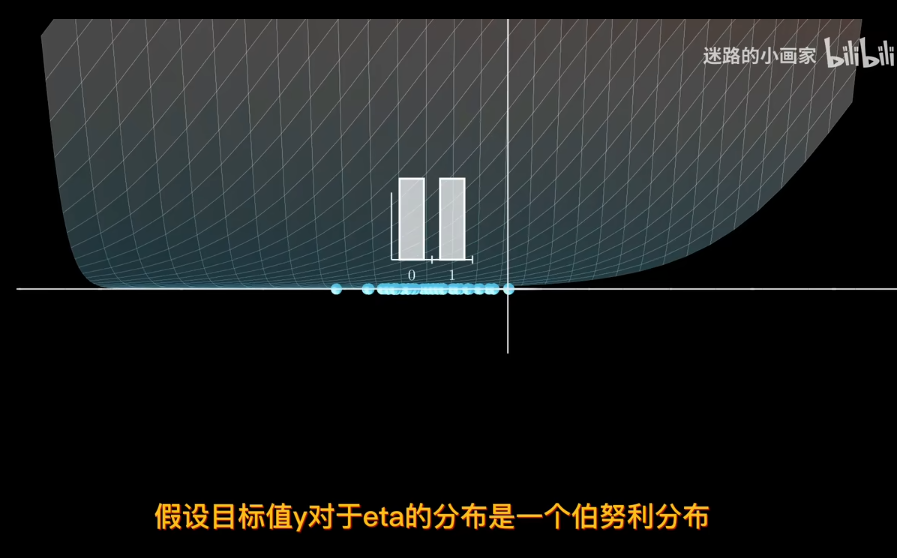
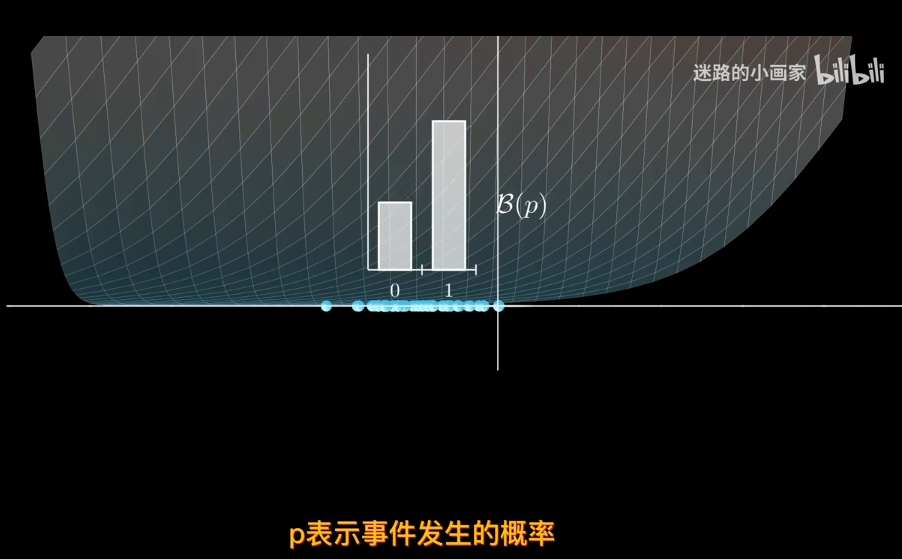
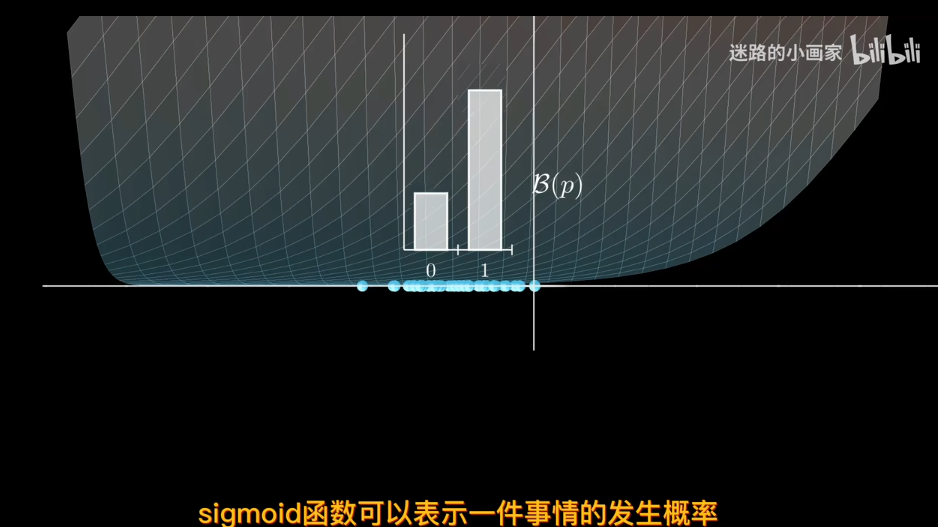
因此sigmod函數可以作爲參數p 對於同分佈獨立數據集，可以用極大似然估計來找到最合適的邊際

SoftMAX

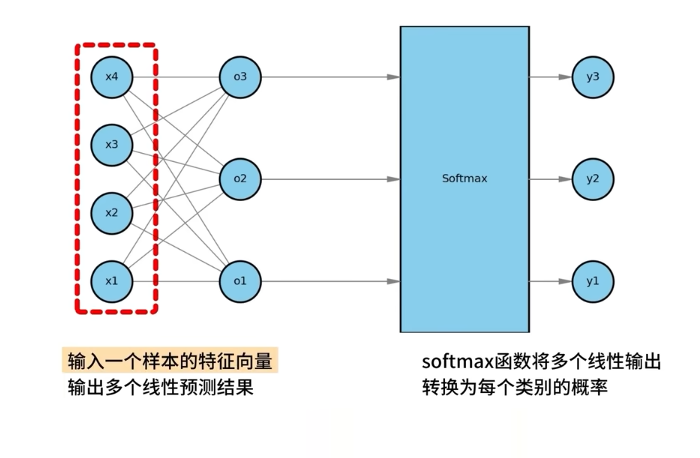
得到O“3*1” 後，輸入o到softmax，得到概率

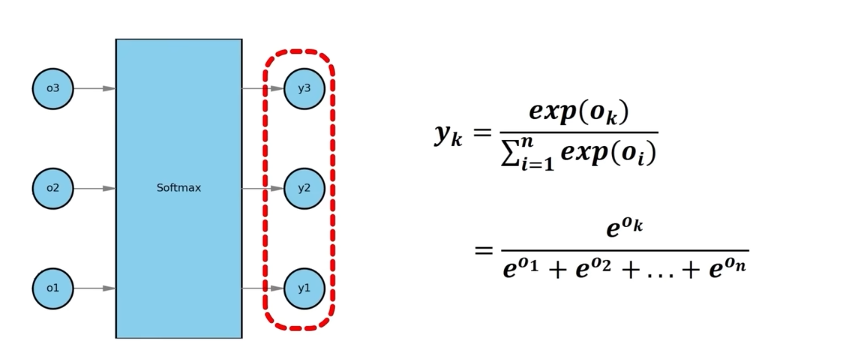
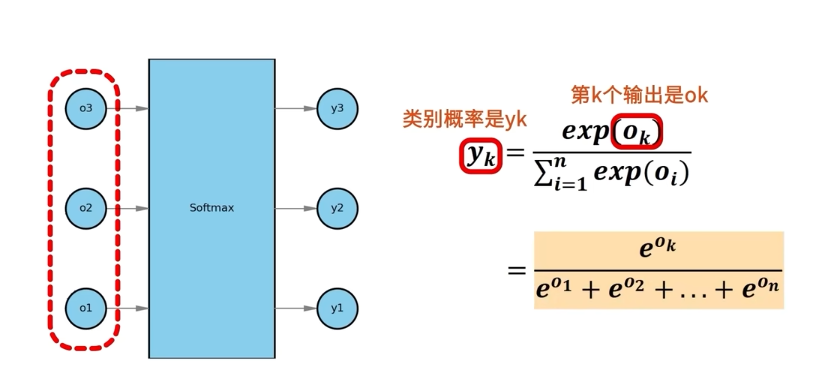
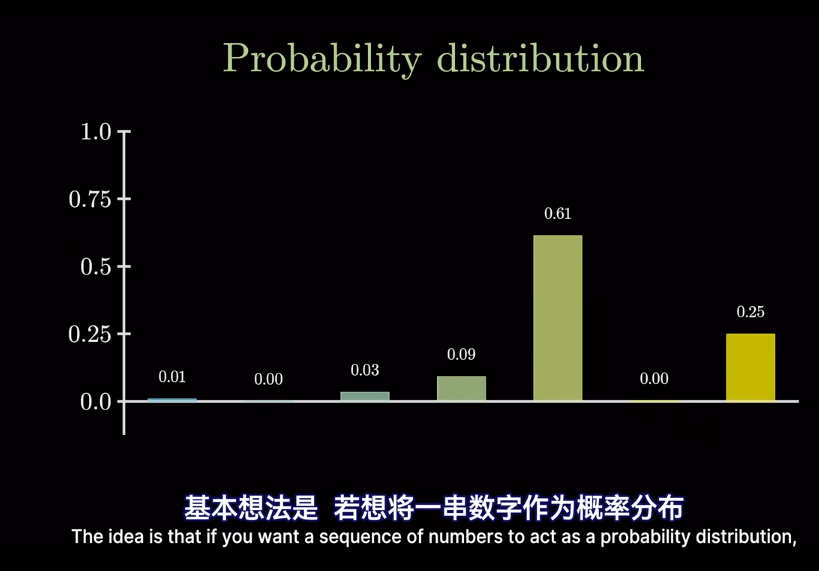
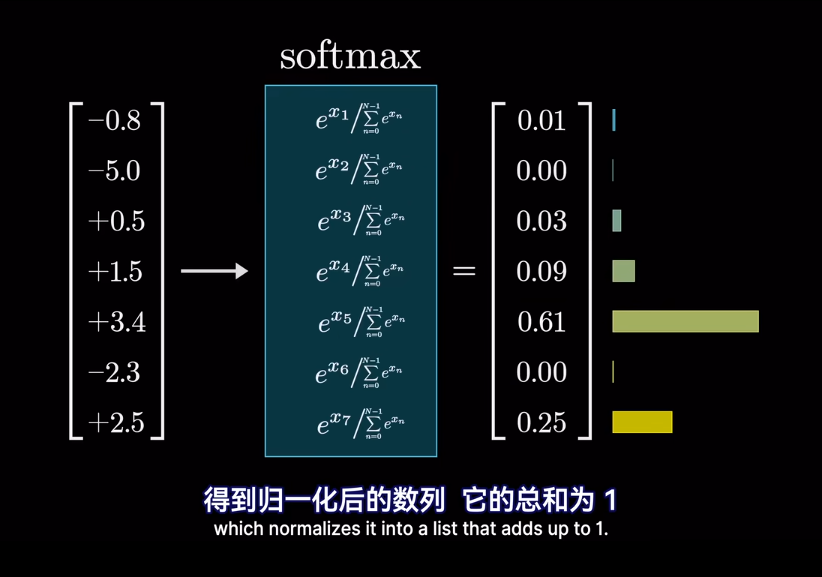經過softmax後，可以保證概率非負，並且總和爲1，也就是所有類別的概率相加爲1

”我們不關心得到的節點值，我們只關心正確的類別值最大“

Transformer

TTV

TTS

TTI

本文介紹的Transformer是如下類型

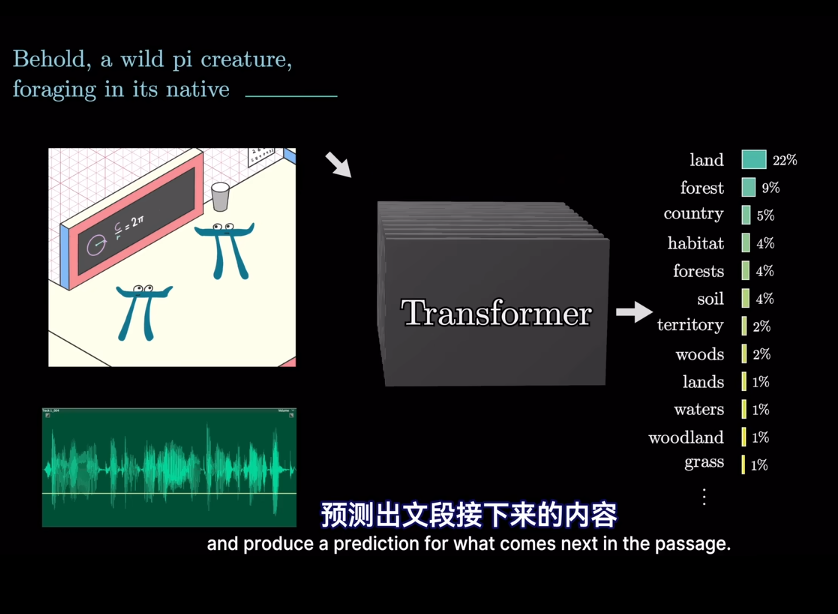
這是爲了編碼該片段的含義 如果將向量看作高維空間座標

在模型的第一層叫做嵌入層

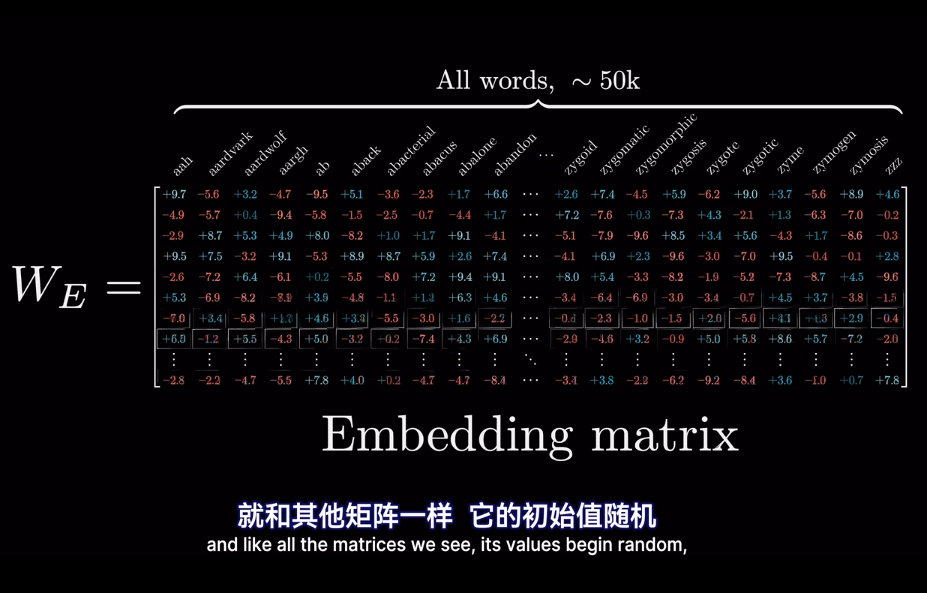
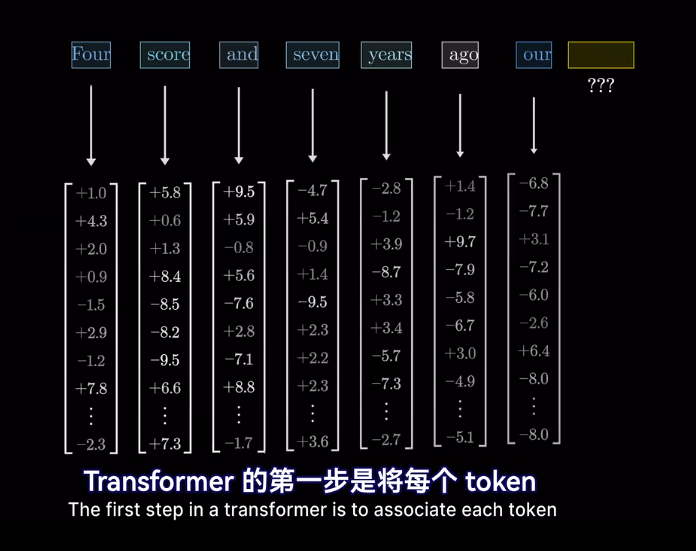
image.png

image.png

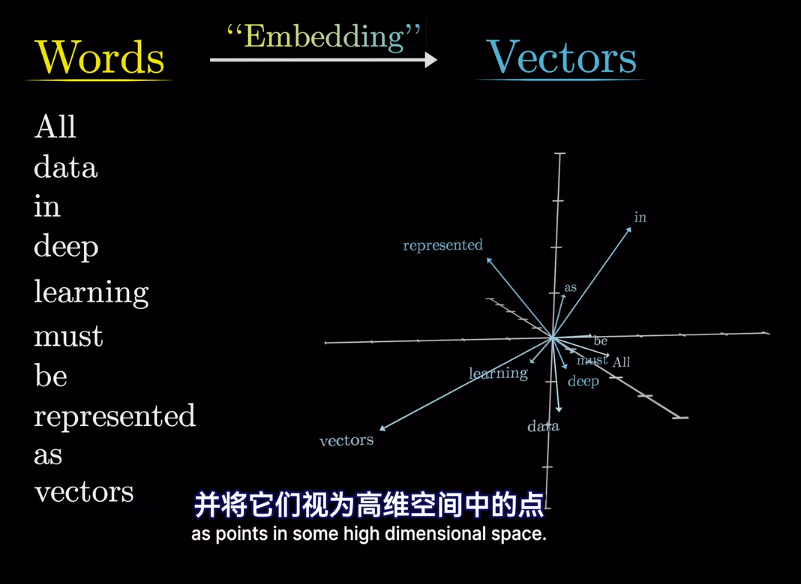
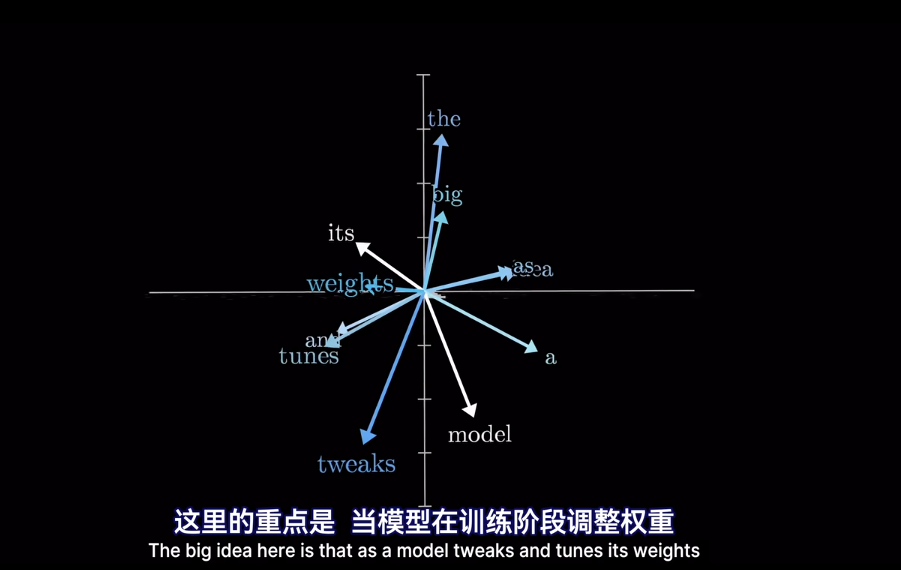
最終的位置會被賦予語義含義

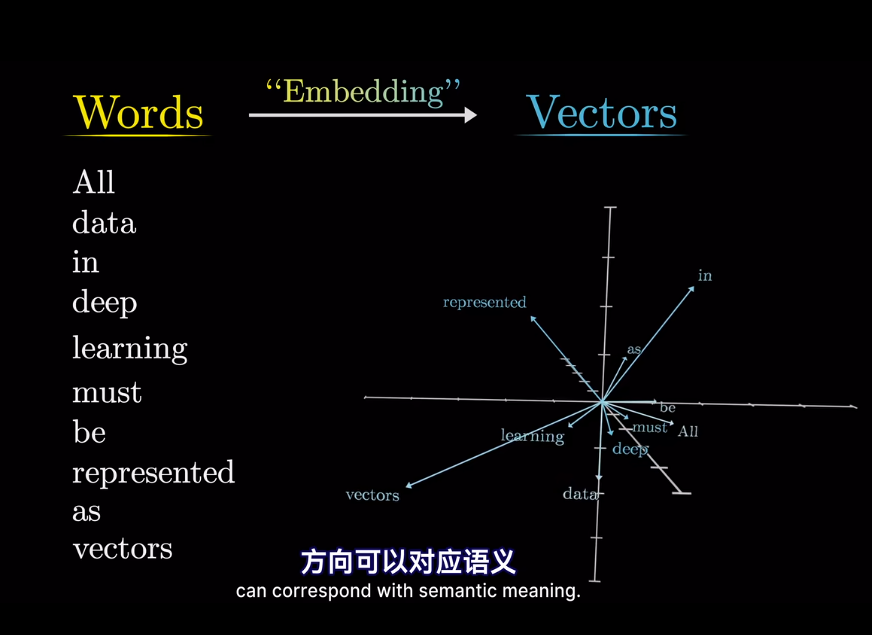
image.png

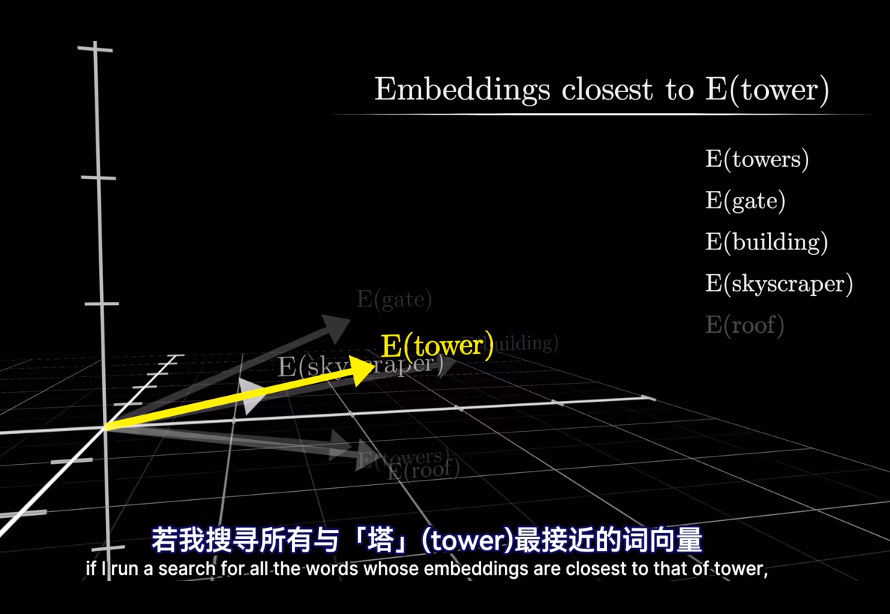
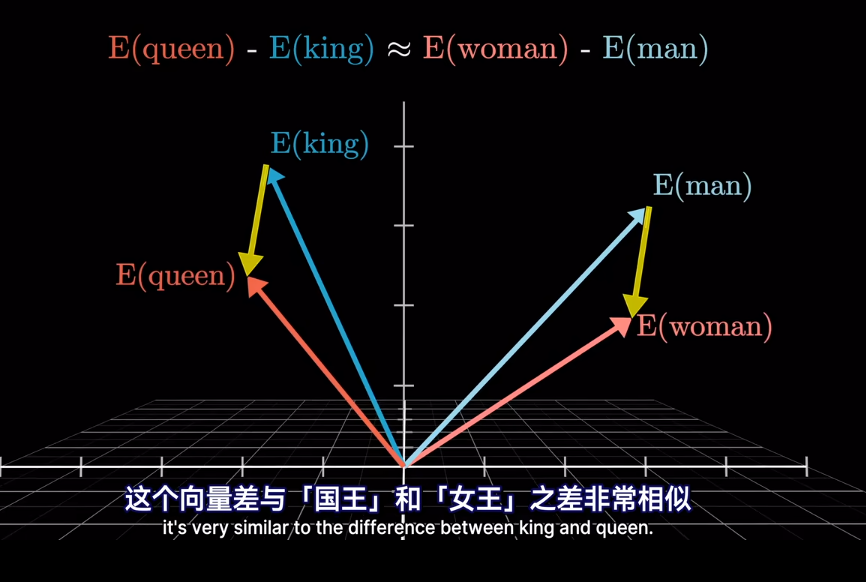
插一句，衡量空間向量接近程度，點乘是個好東西

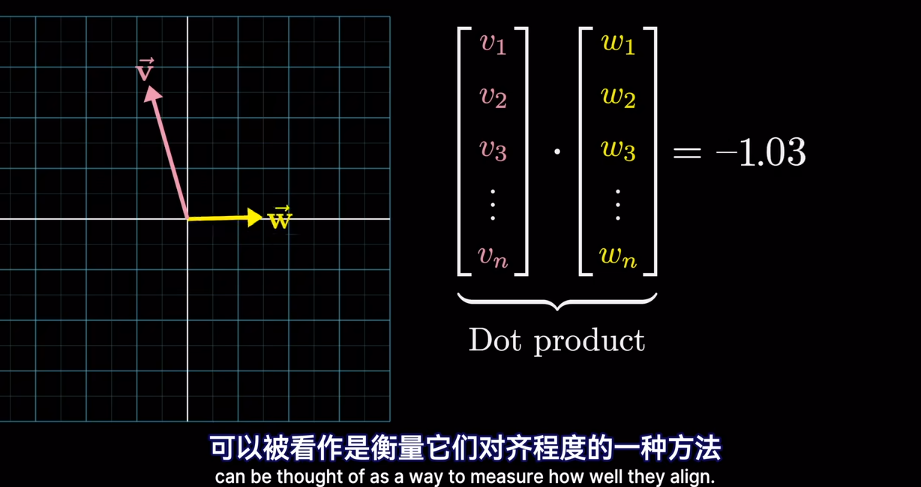
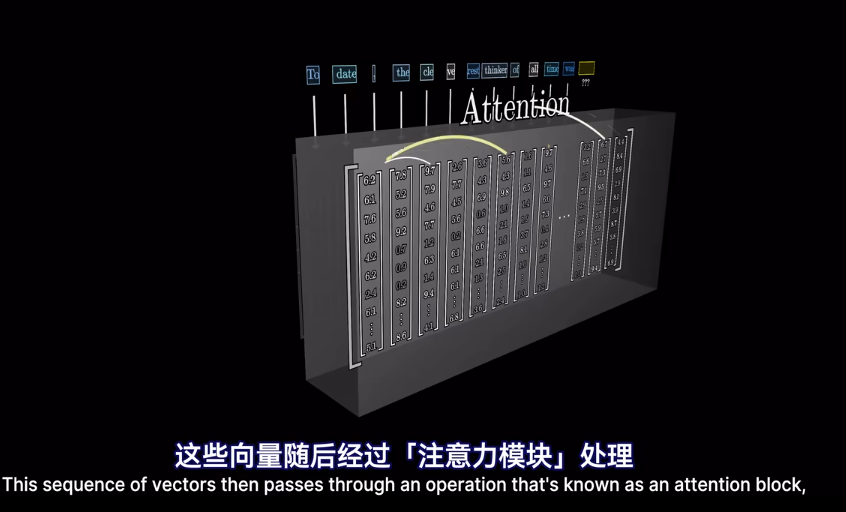
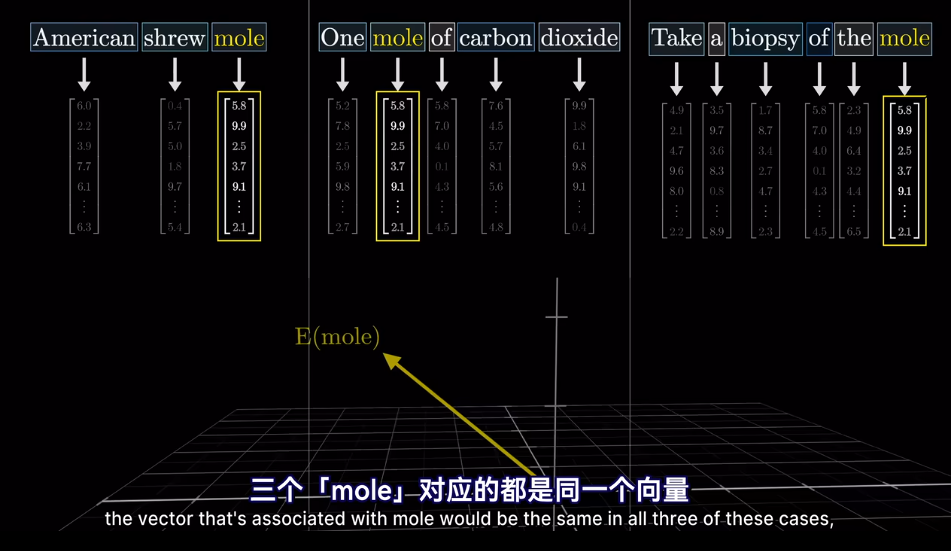
meaning 已經被編碼爲向量，但是在不同的上下文中，語義會改變

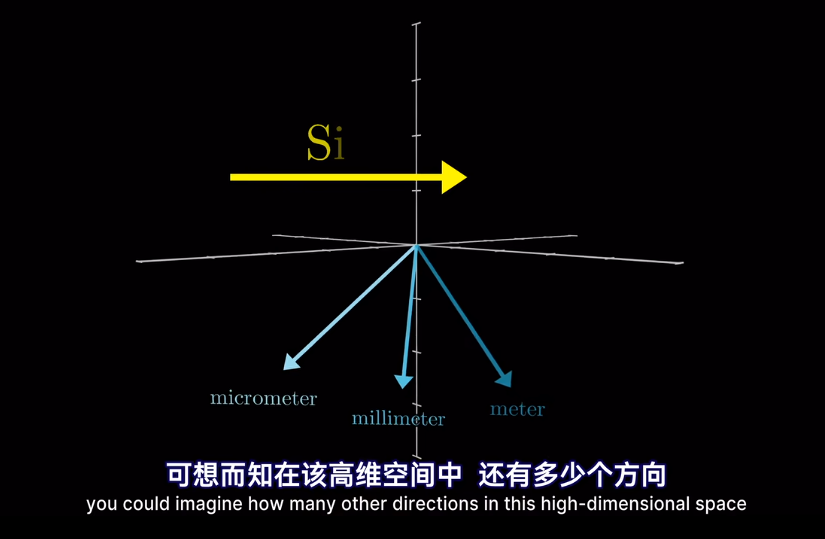
image.png

image.png

這裏需要注意在嵌入矩陣沒有上下文

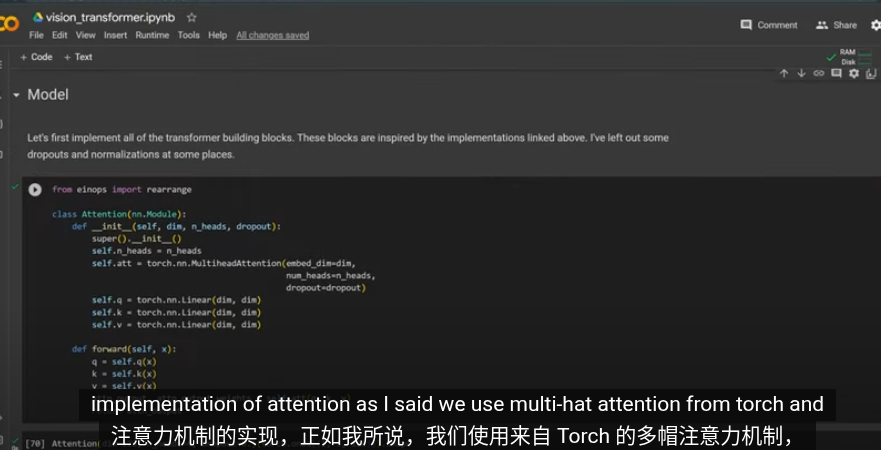
image.png

image.png

self-attention

在經過attention後

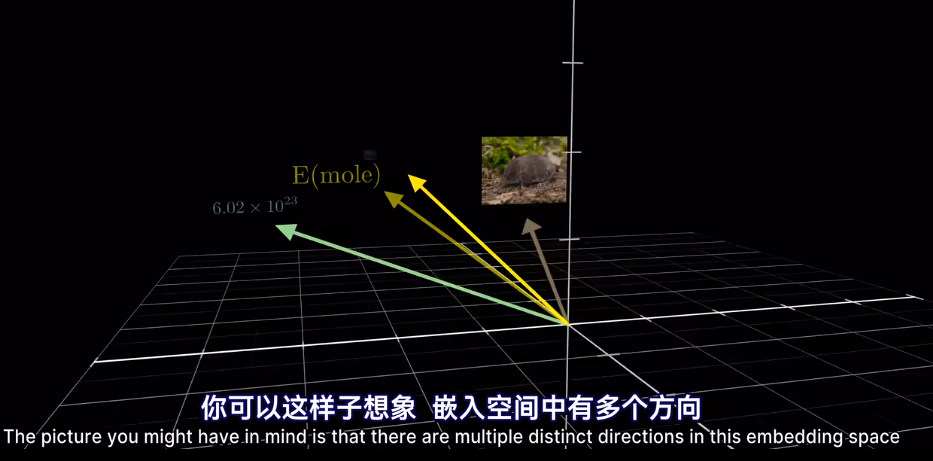
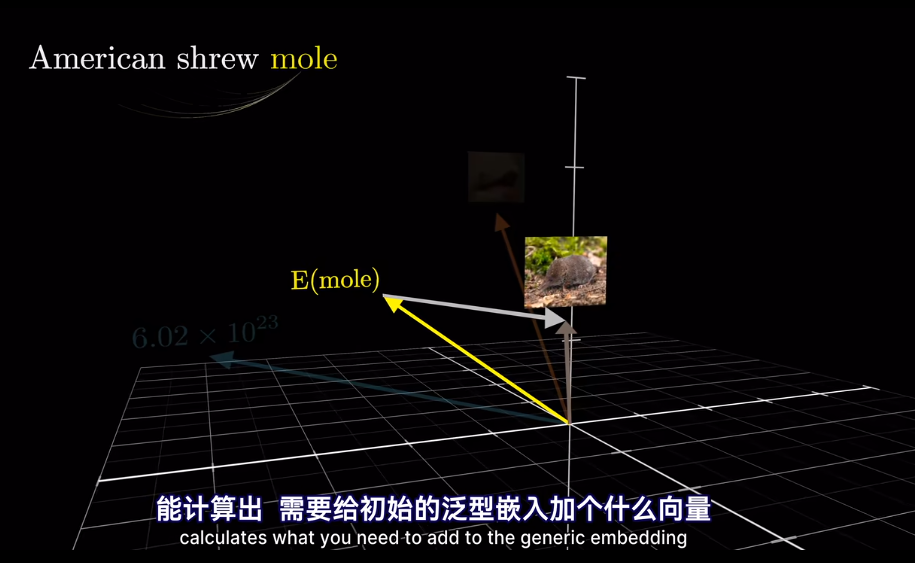
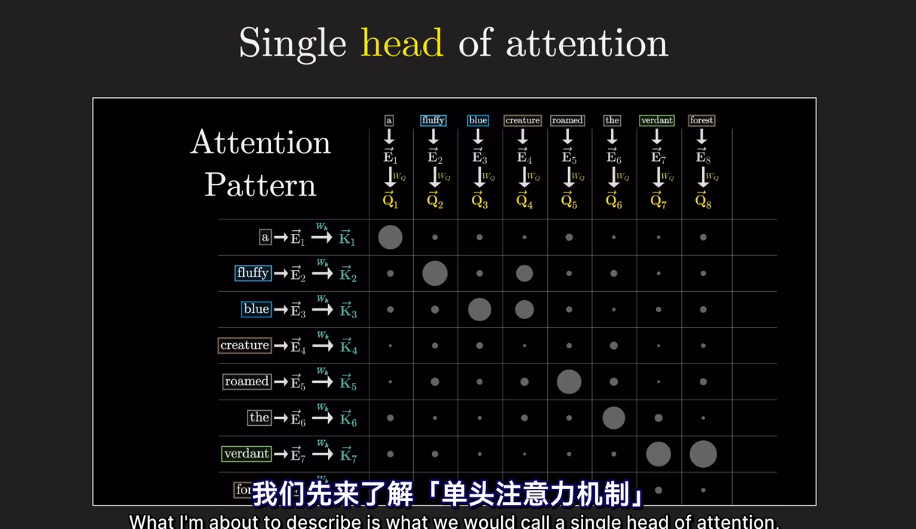
image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png

其實在最開始不只是編碼了詞的含義

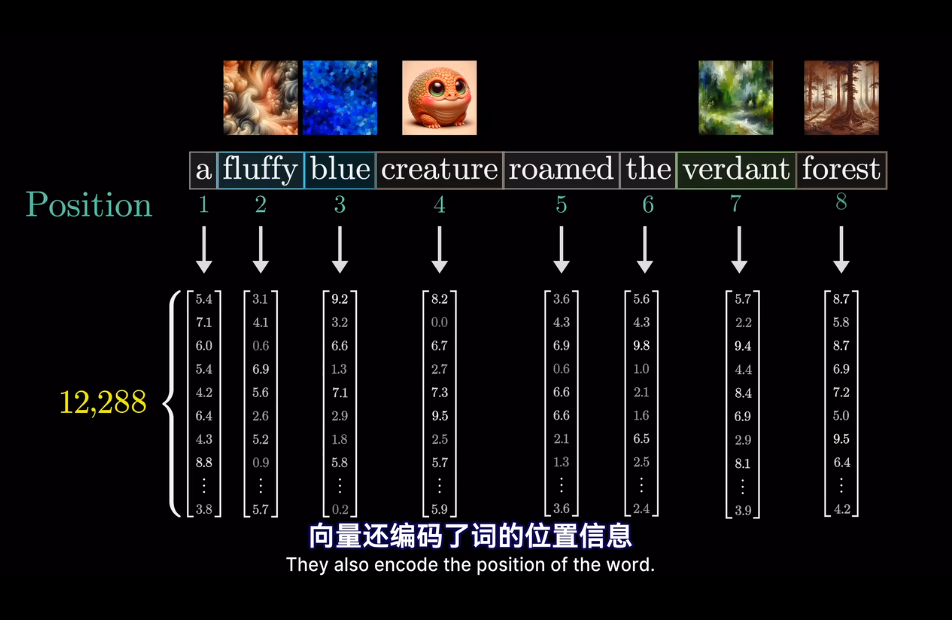
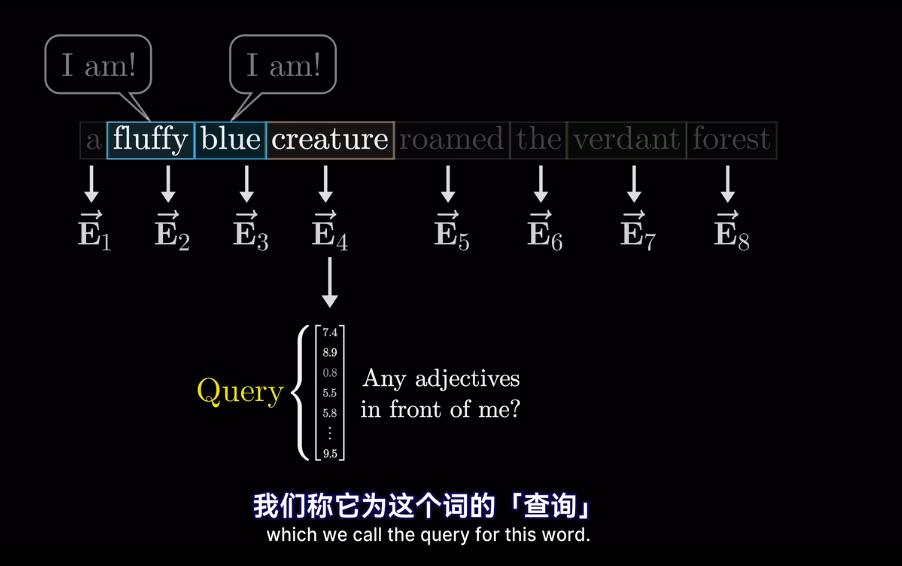
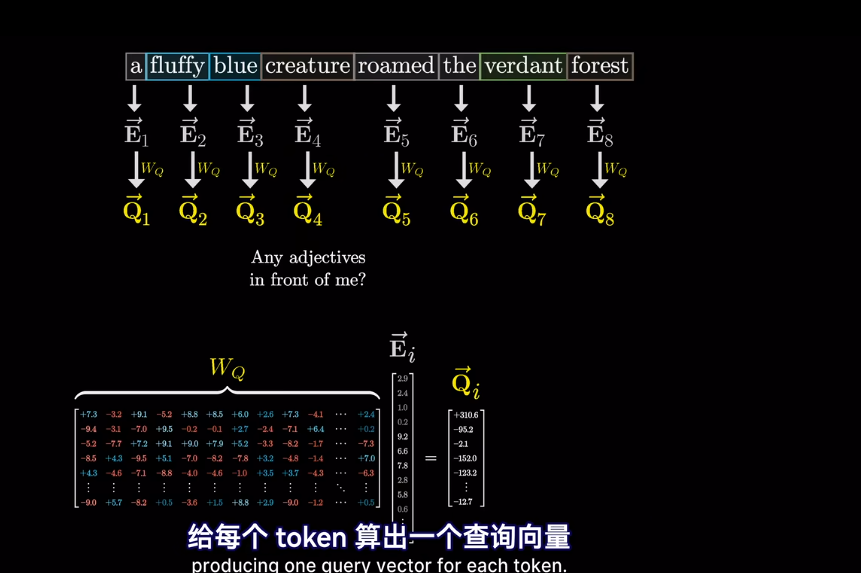
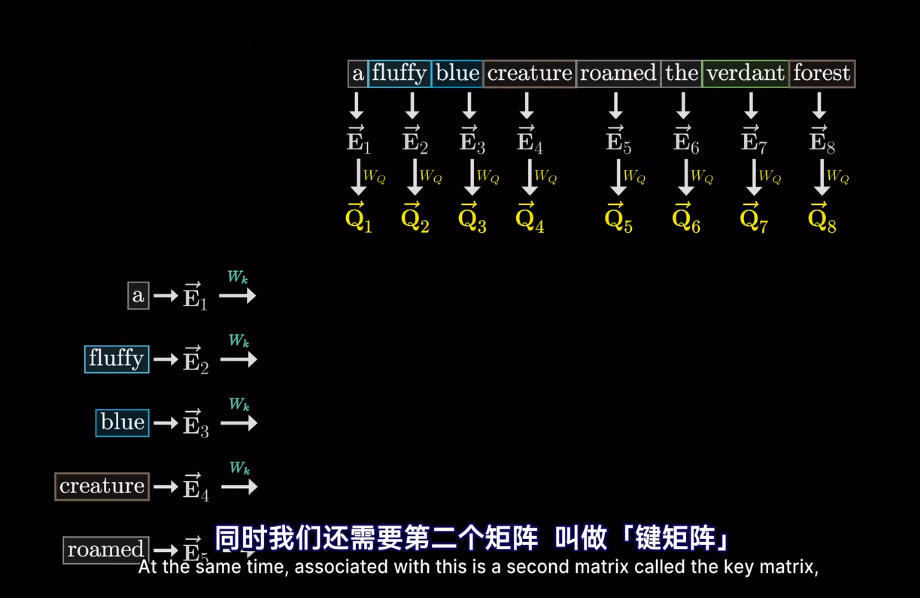
image.png

image.png

image.png

image.png

image.png

會將高維的詞映射到低維空間

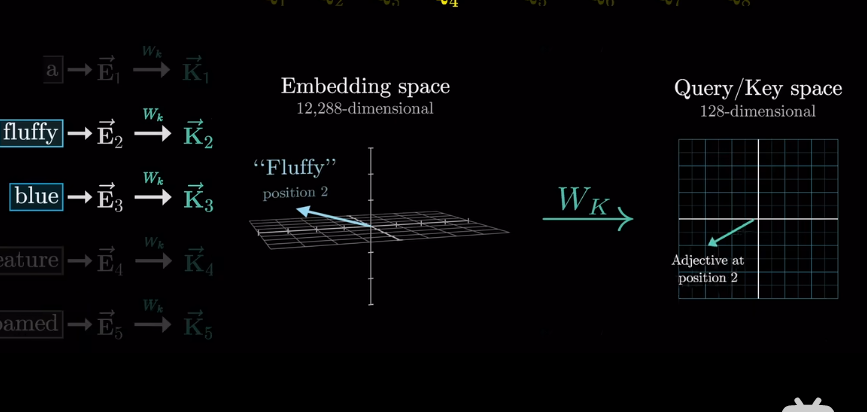
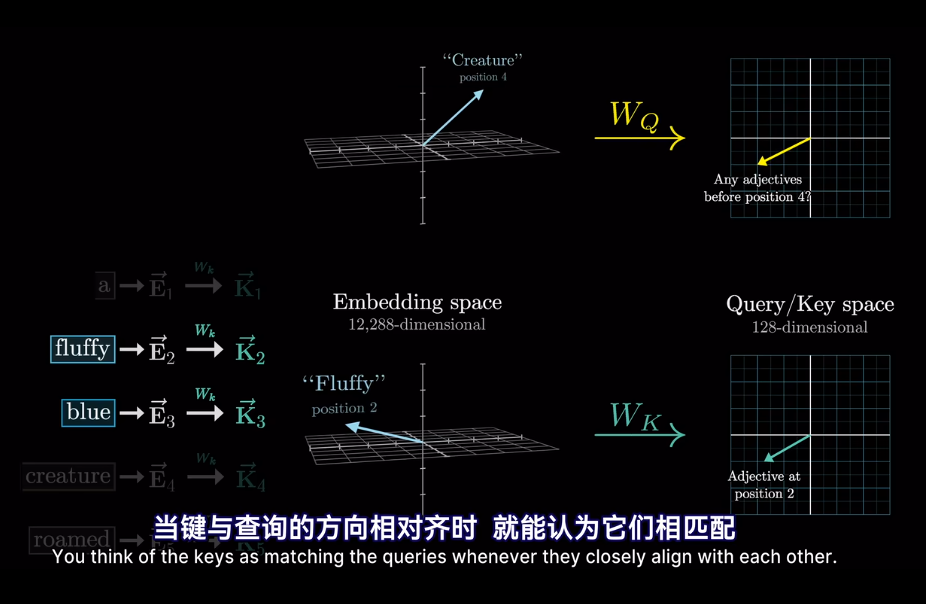
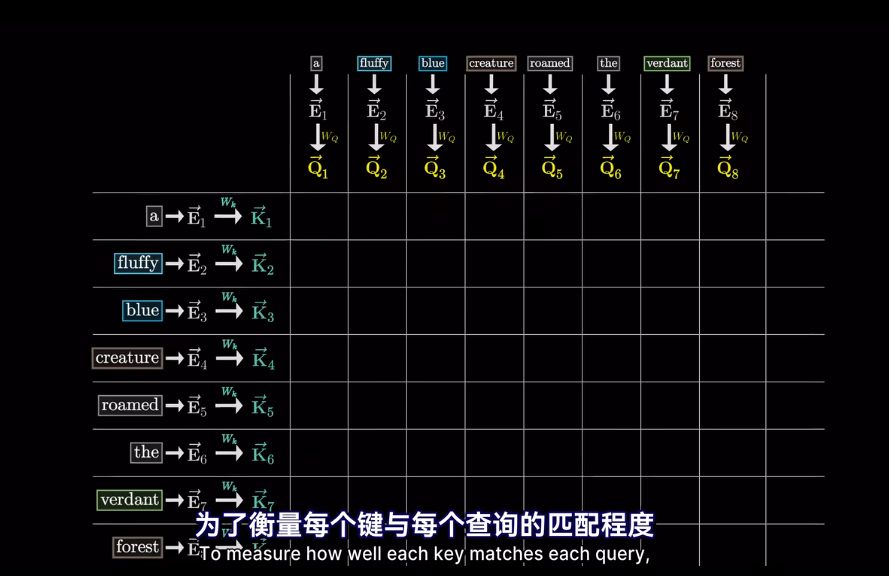
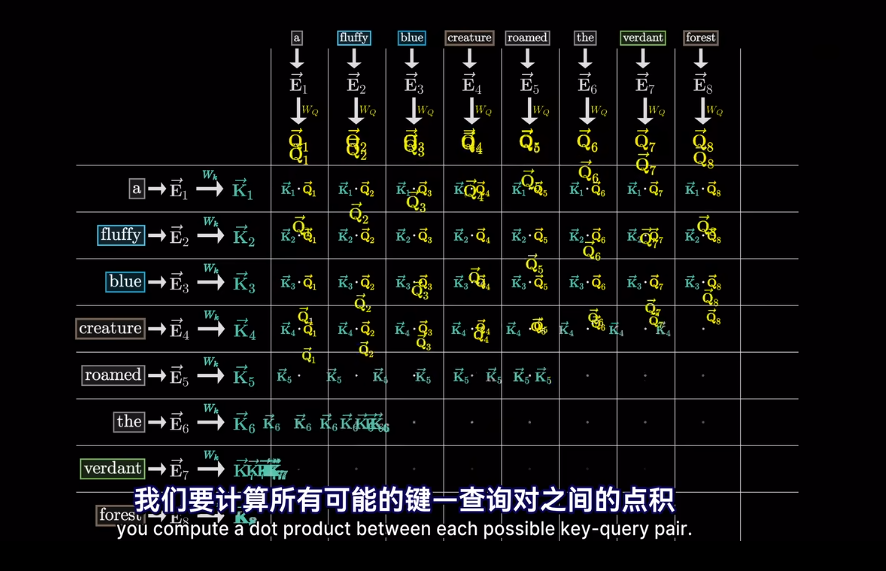
image.png

image.png

image.png

image.png

image.png

image.png

但我們想要的是概率或者說，相關度，也就是最可能關聯的詞。不是單純的數值

softmax

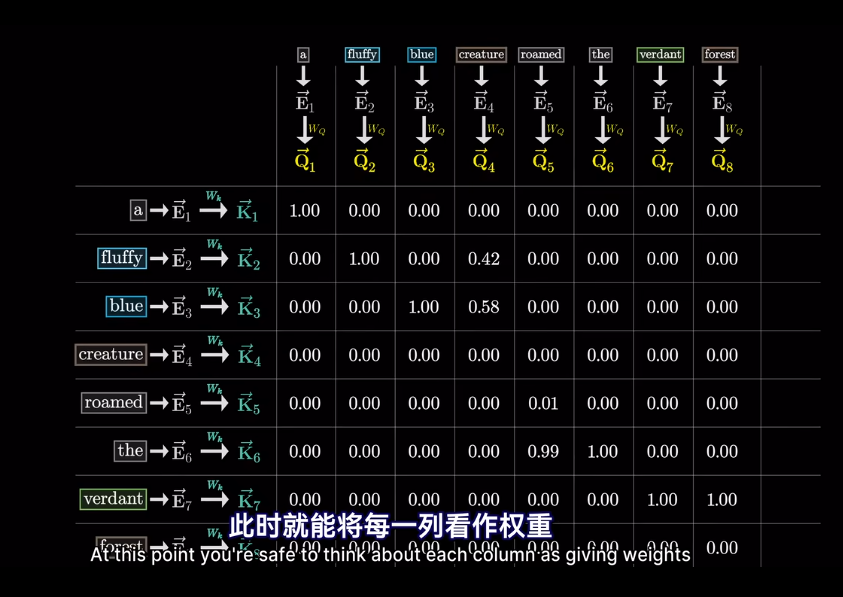
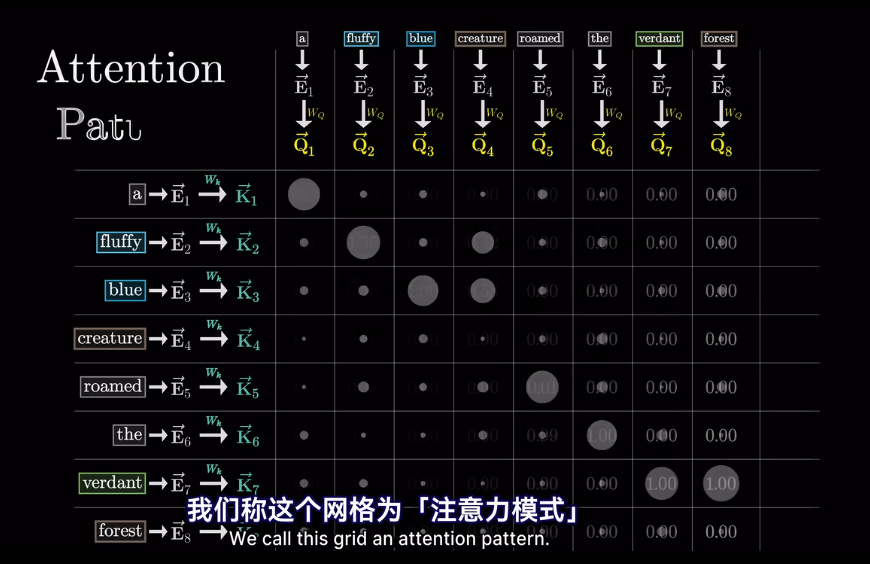
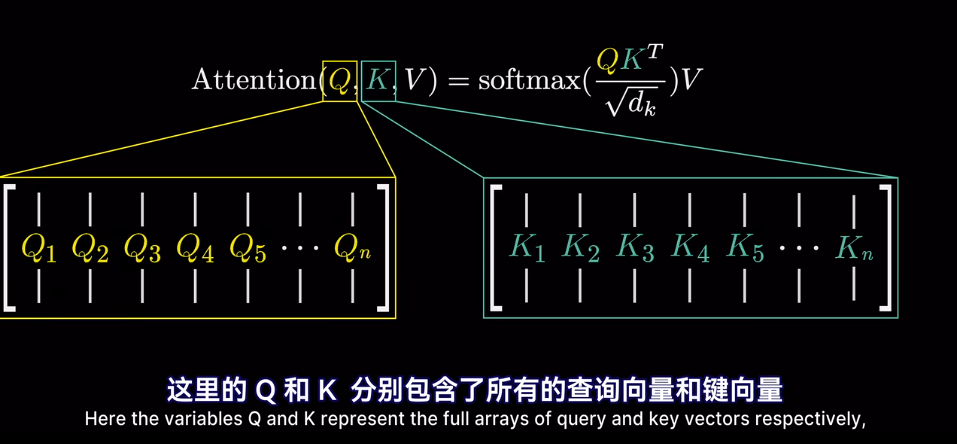
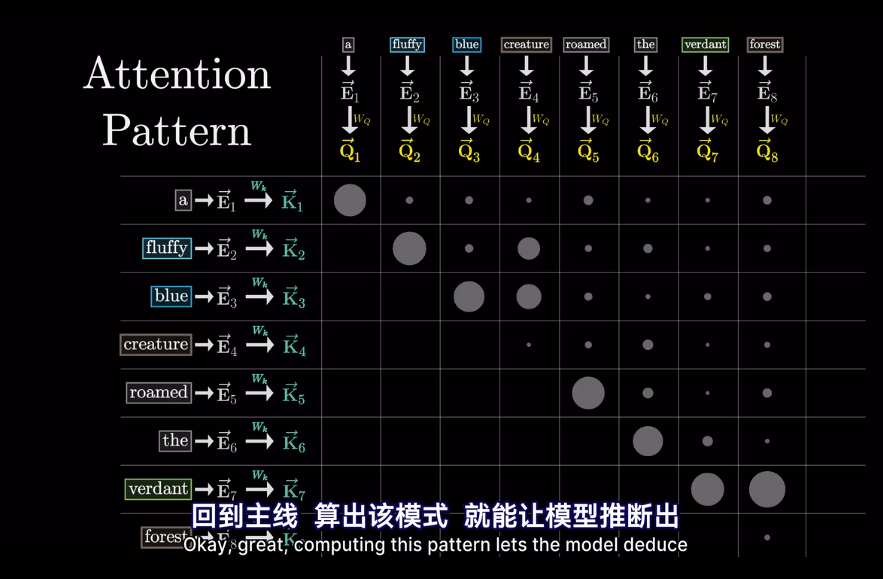
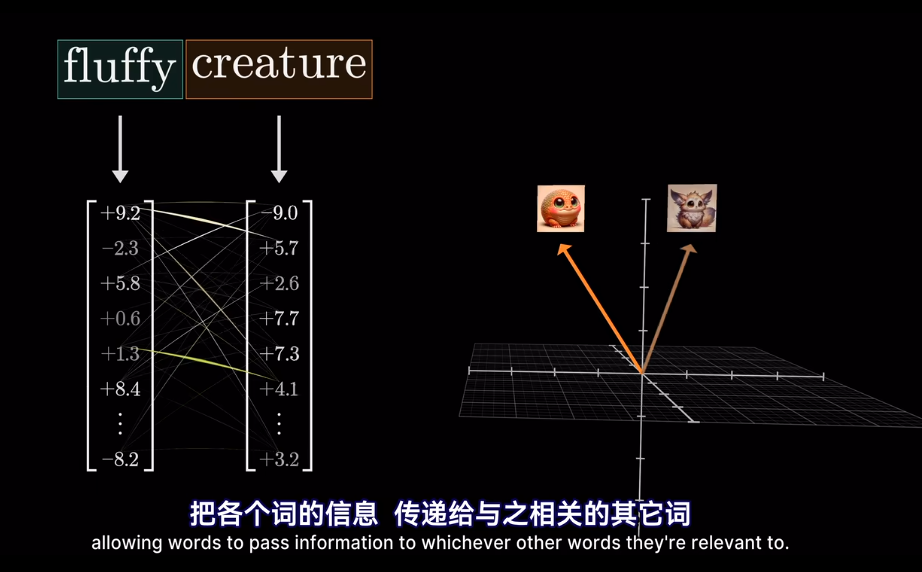
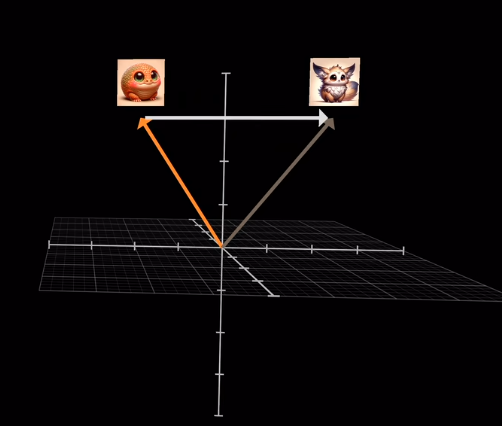
image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png image.png

image.png

image.png

image.png

image.png

然後求softmax概率，歸一化

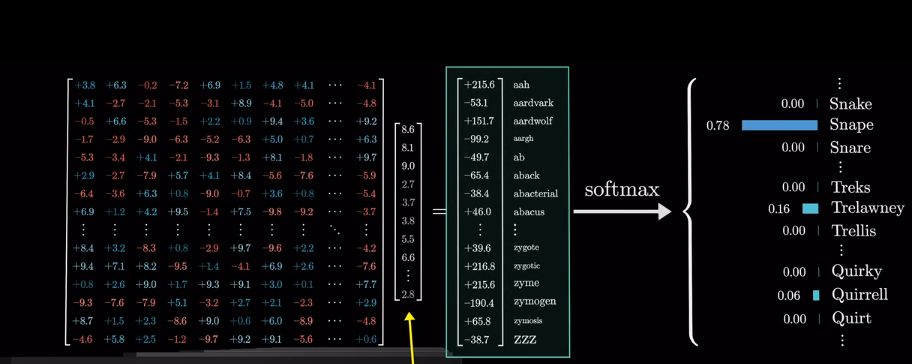
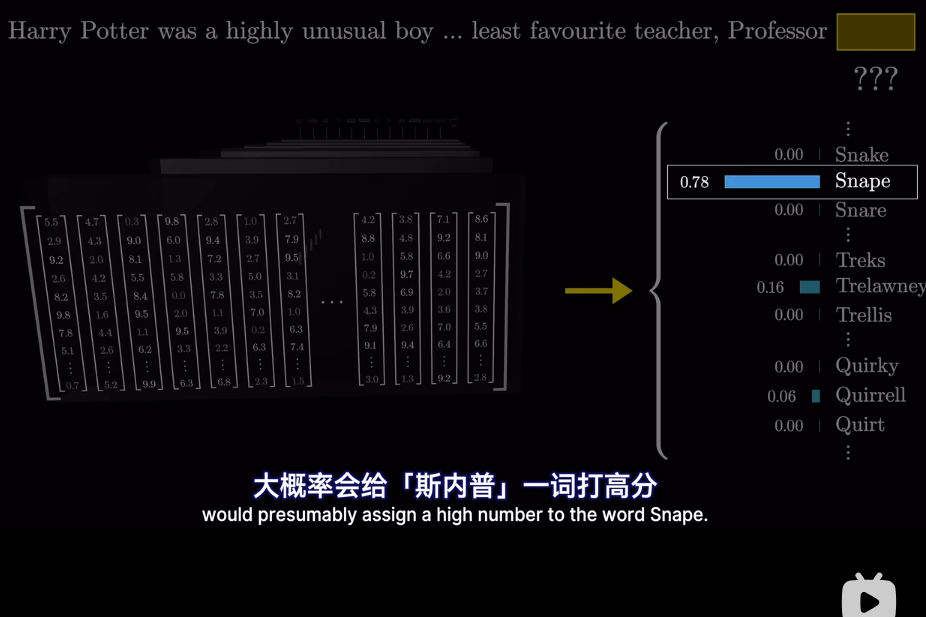
但是爲什麼只用最後一個向量？

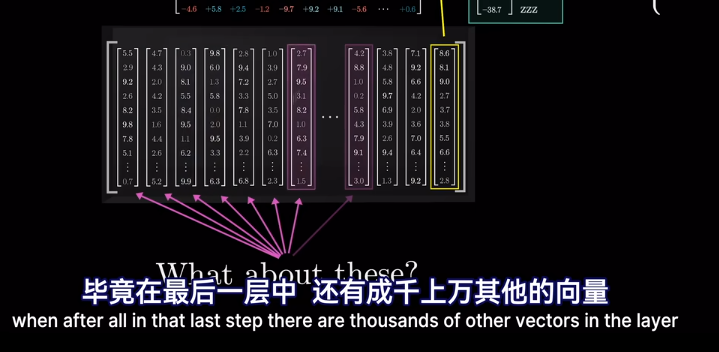
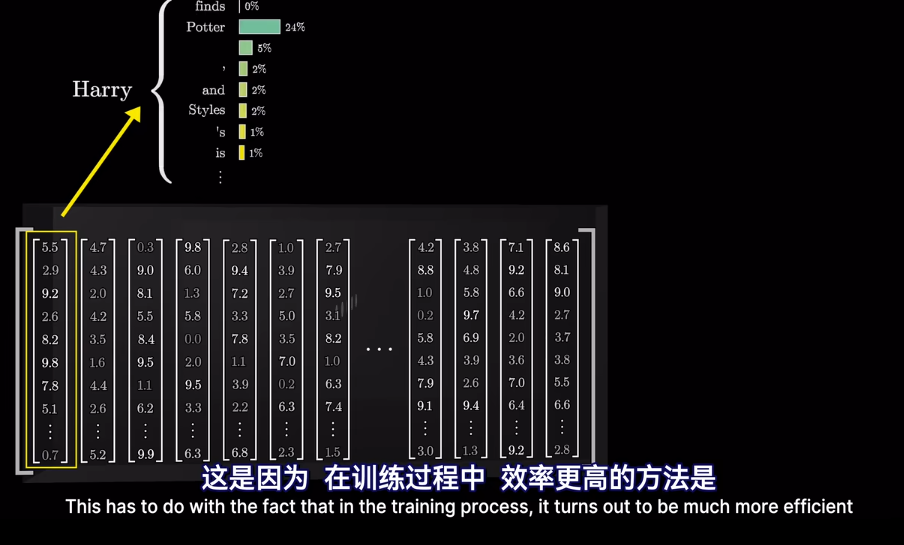
Vsion Transformer

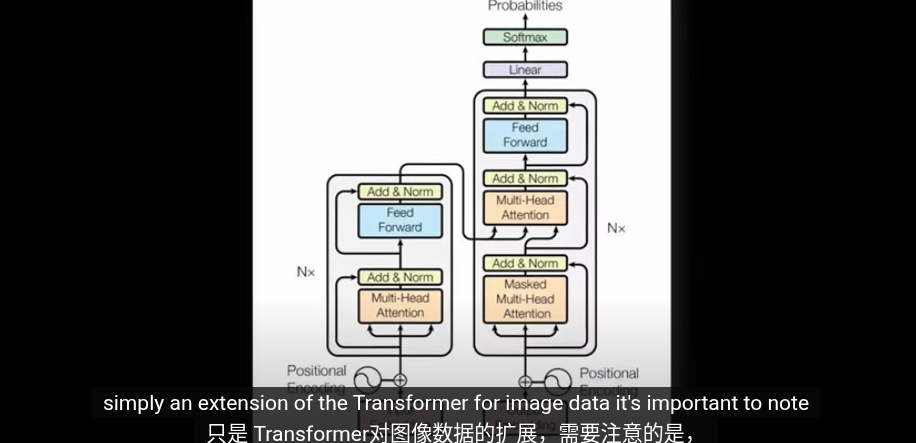
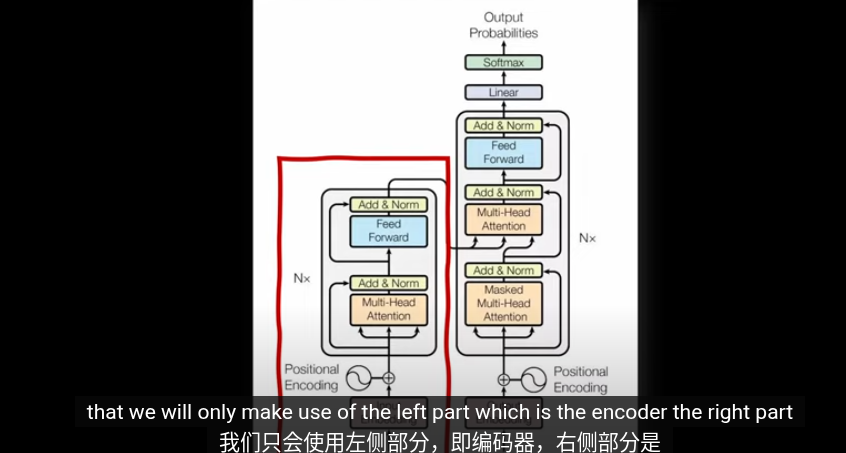
image.png

image.png

第一步，圖片編碼爲嵌入向量。目的和Transformrer中的嵌入空間類似爲了將相似的圖片放到接近的位置，並給高維空間的圖片賦予含義

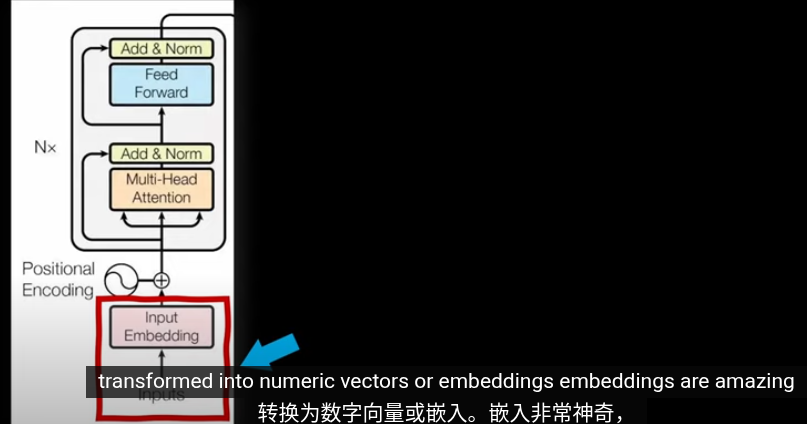
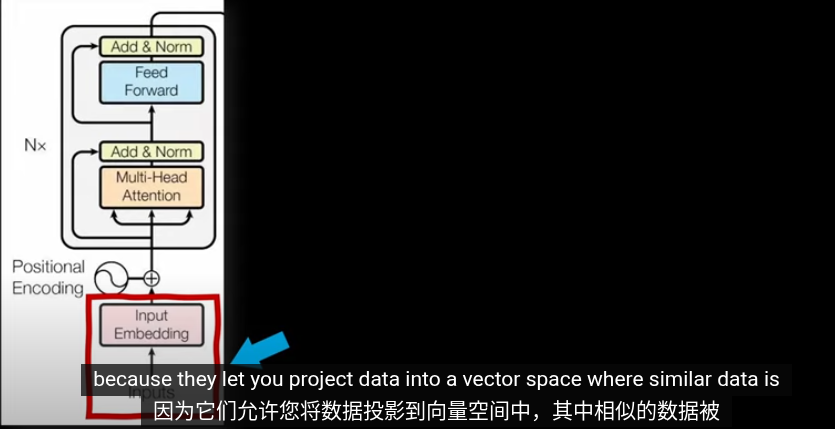
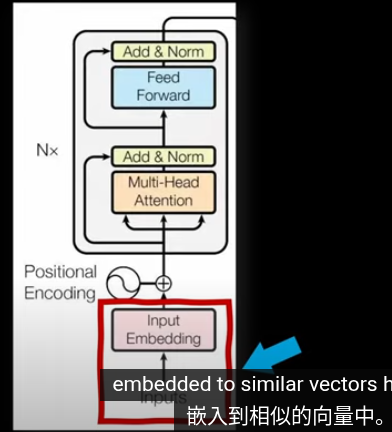
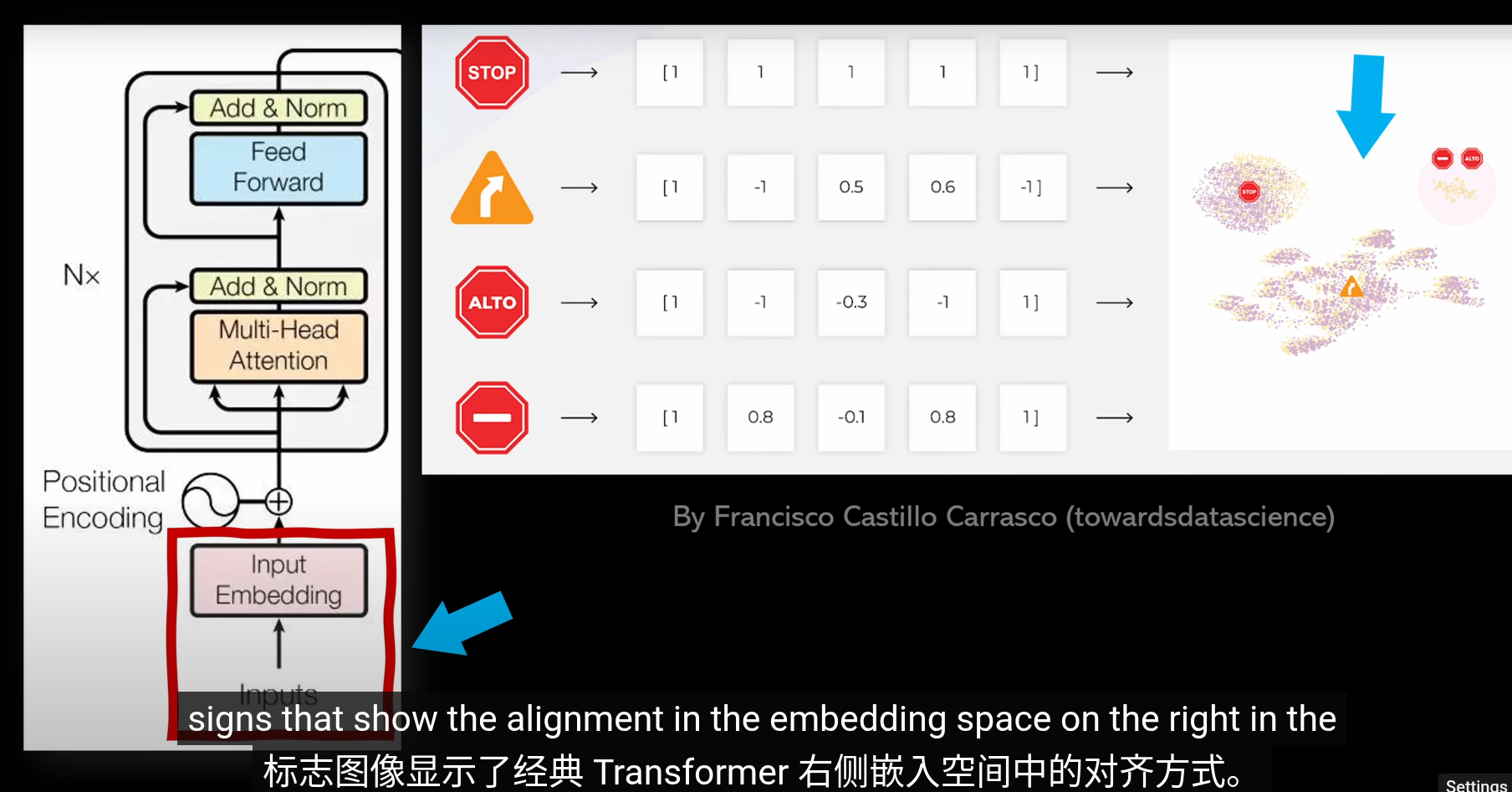
image.png

image.png

image.png

image.png

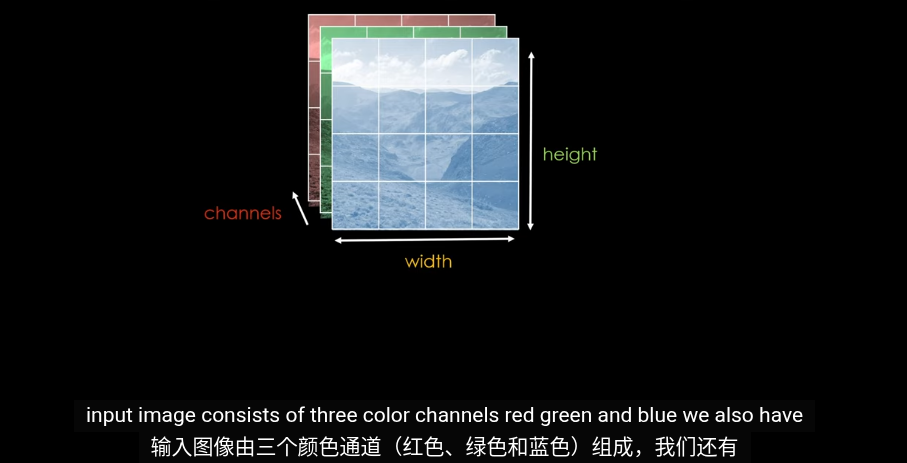
但是傳統的Trasformer用於NLP，輸入就是拆分語句形成零碎的單詞以及對應的Token，我們怎麼從圖片裏提取Token？ image.png

image.png

image.png image.png image.png

我們使用 inops 來 reshape 也就是切割

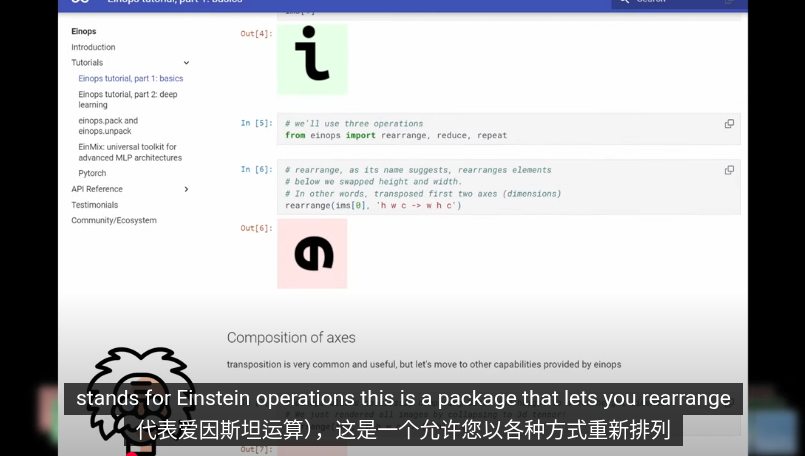
image.png

image.png

image.png

image.png

image.png

image.png

有時爲了效率可以用CNN代替

代碼

數據集 劍橋動物3 圖片調整爲統一大小，轉爲 tensor

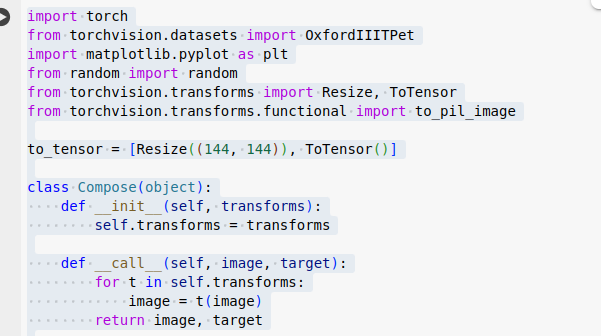
image.png

image.png

做 inops 操作，展平特徵，輸入線性層裏得到patch embedding 嵌入向量

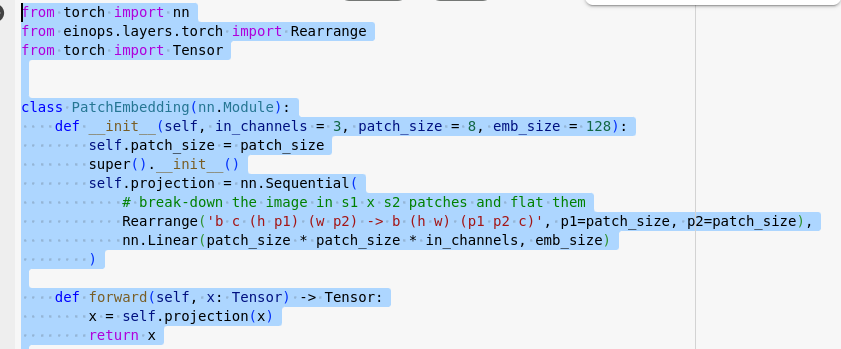
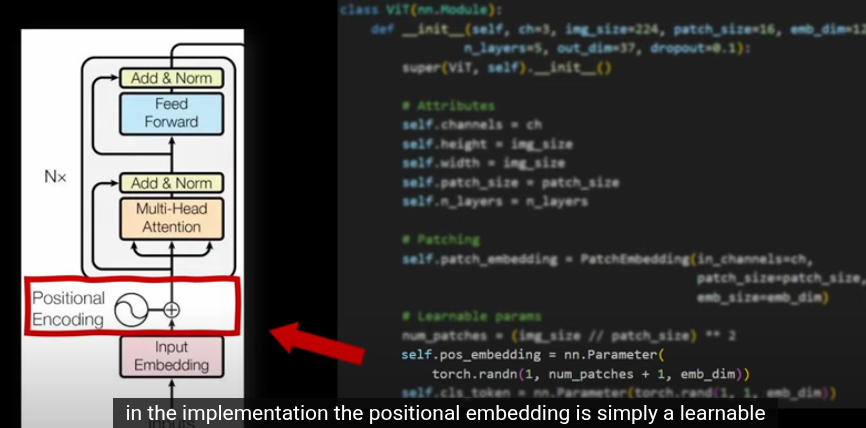
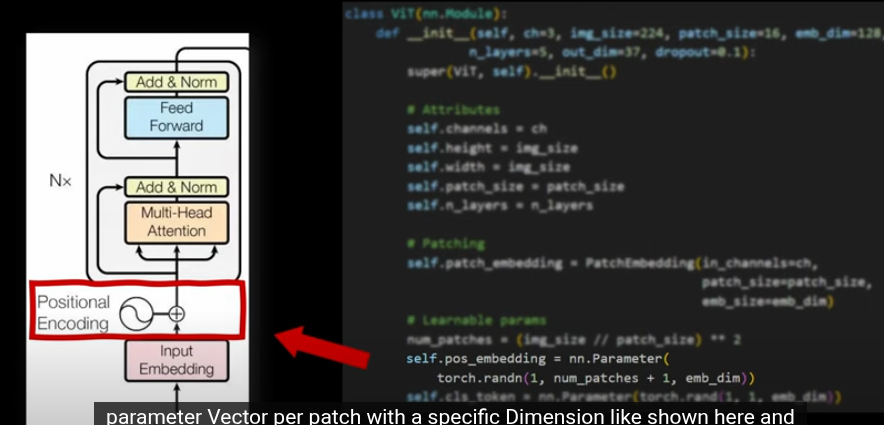
image.png

image.png

image.png

image.png

image.png

image.png

image.png

加入位置編碼後，就是經典的transformer了

image.png

image.png

image.png

image.png

image.png

image.png

Knowledge Distillation

image.png

關於 model compression 模型壓縮

image.png

image.png

因爲模型大小的原因，很多模型並未轉化爲實際應用。因爲計算資源，內存是有限的

image.png

目前在擴大規模訓練上成果顯著

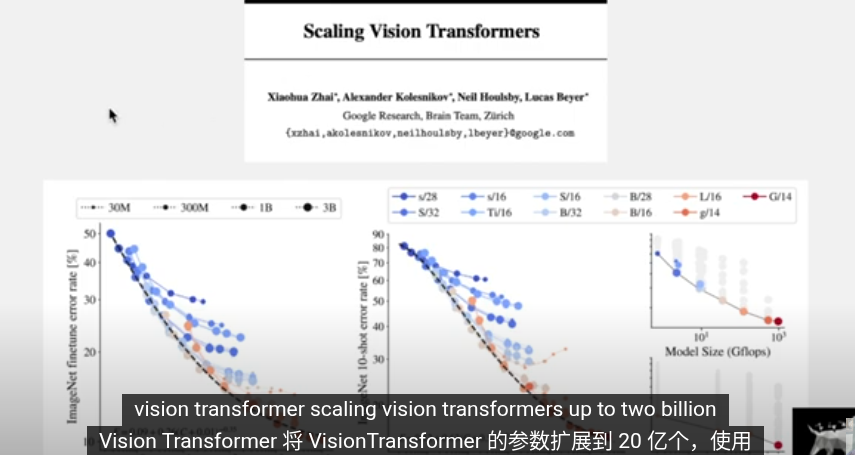
image.png

image.png

image.png

這存在許多問題

我們把重點放在知識蒸餾

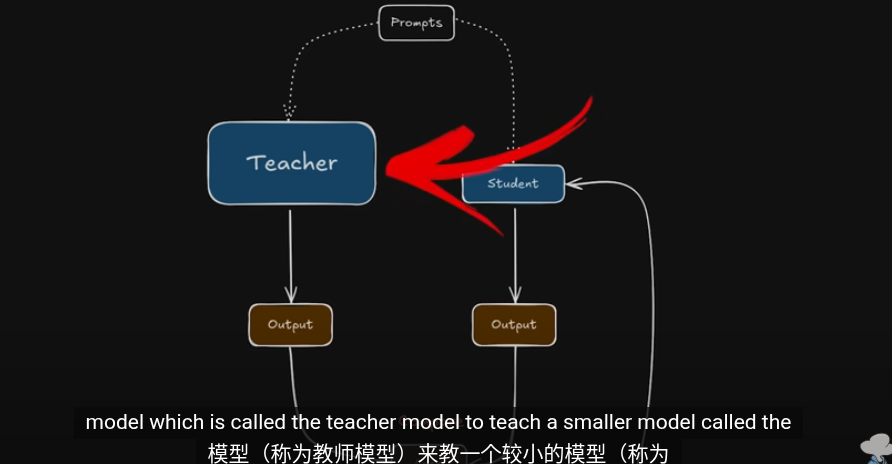
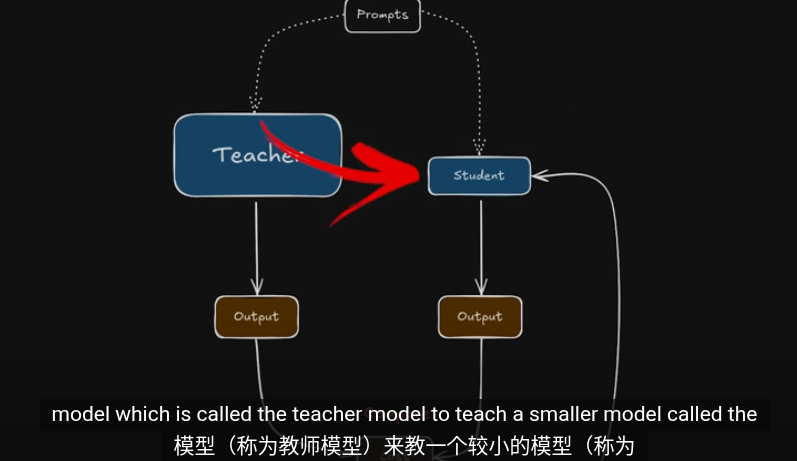
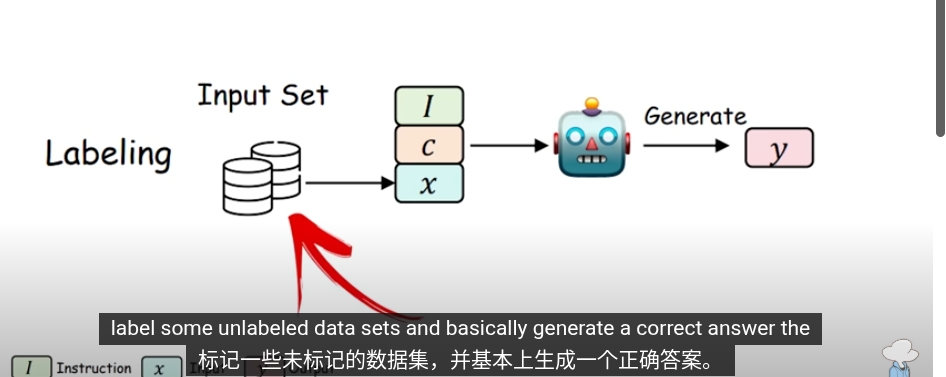
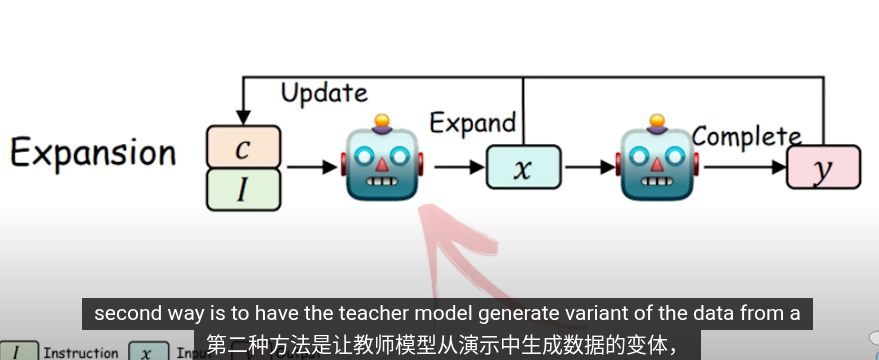
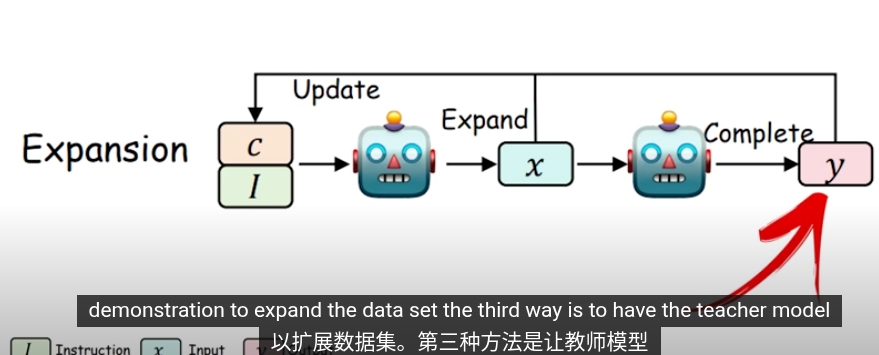
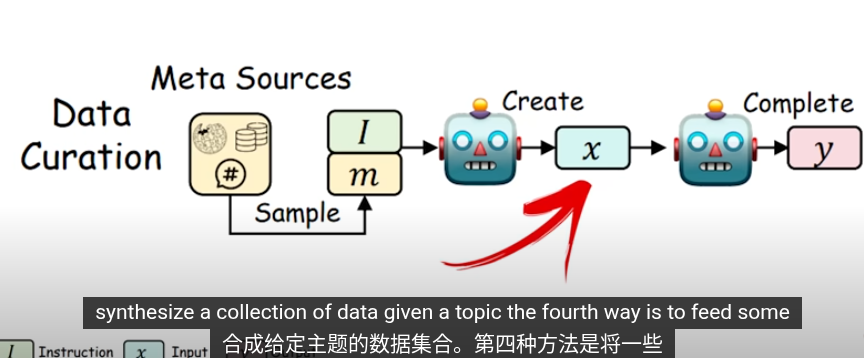
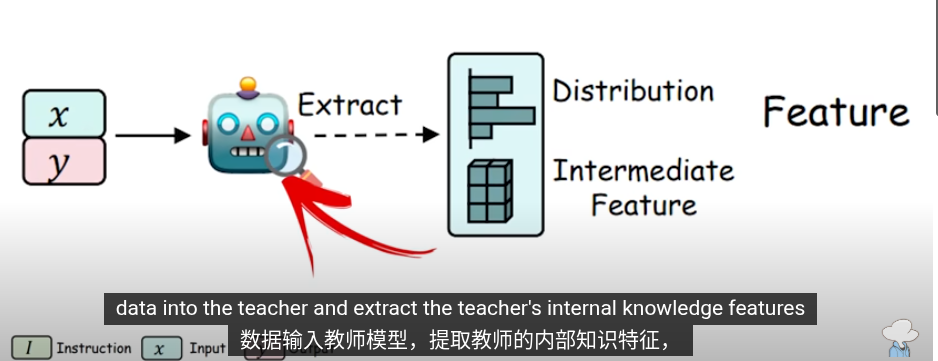
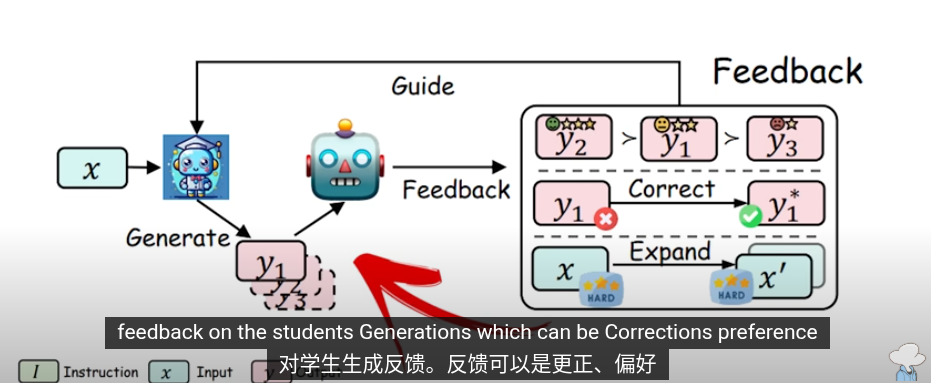
image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png

這些是知識提取的方法，把提取的知識用於下一輪的訓練

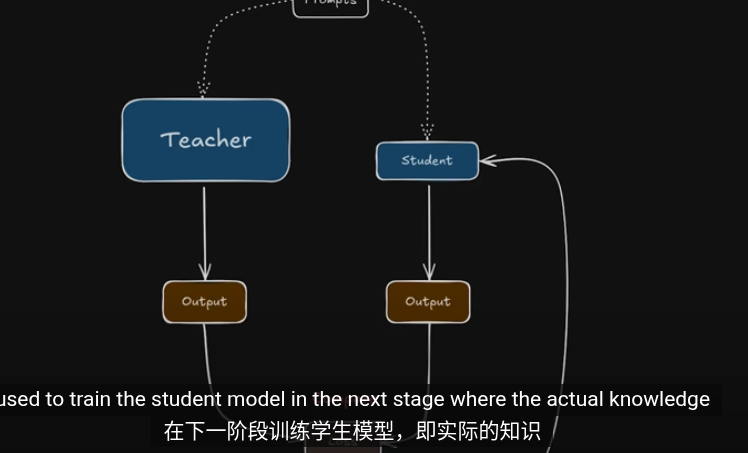
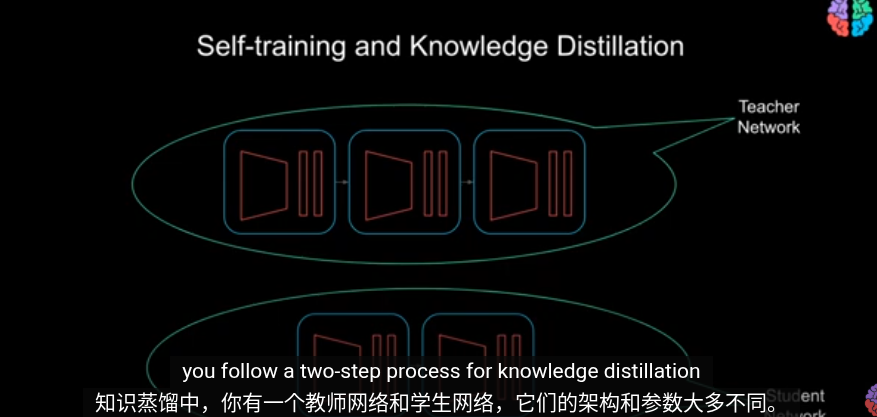
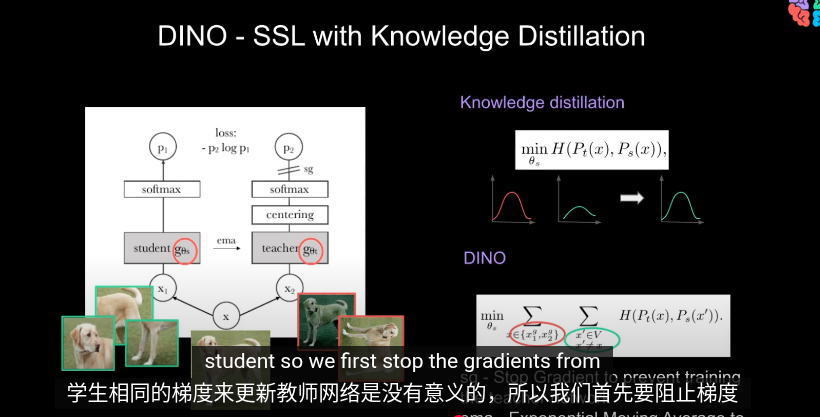
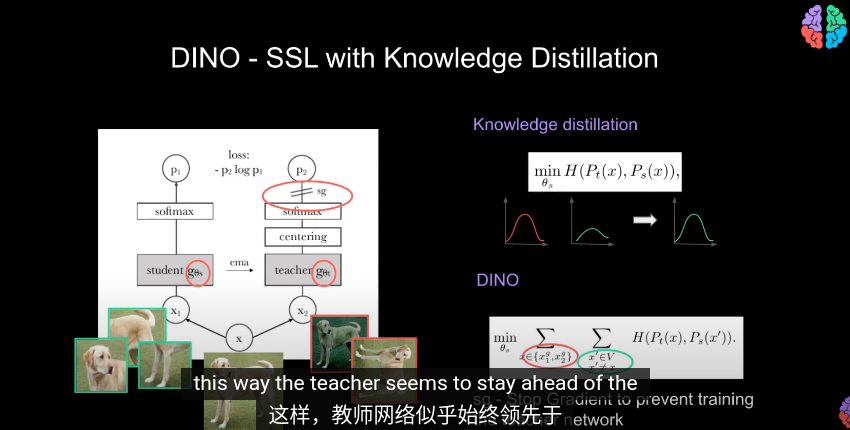
image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png

在知識蒸餾，使用交叉商來最小化輸出概率

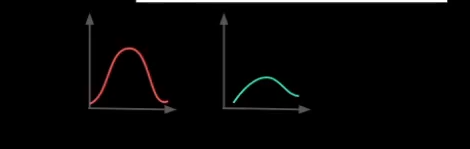
image.png

Centering 中心化

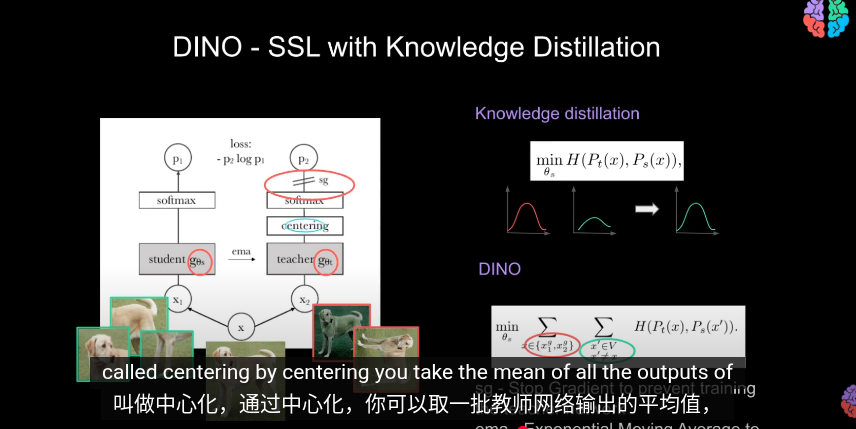
image.png

image.png

image.png

image.png

image.png

DINO

一中新的自監督學習方法

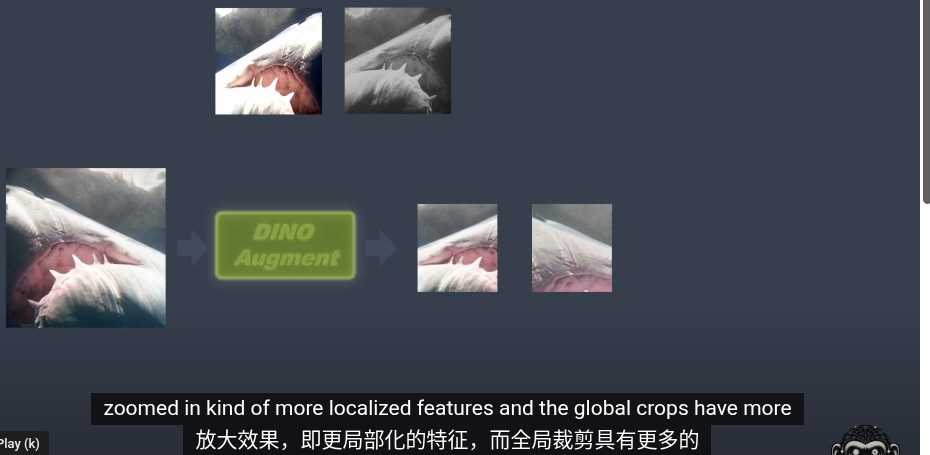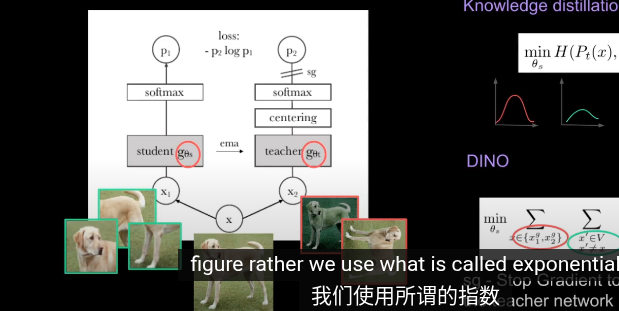
image.png

image.png

image.png

image.png

image.png

image.png

image.png====

dino 與知識蒸餾的不同之處是

image.png

image.png

其中教師網絡會與學生一同訓練

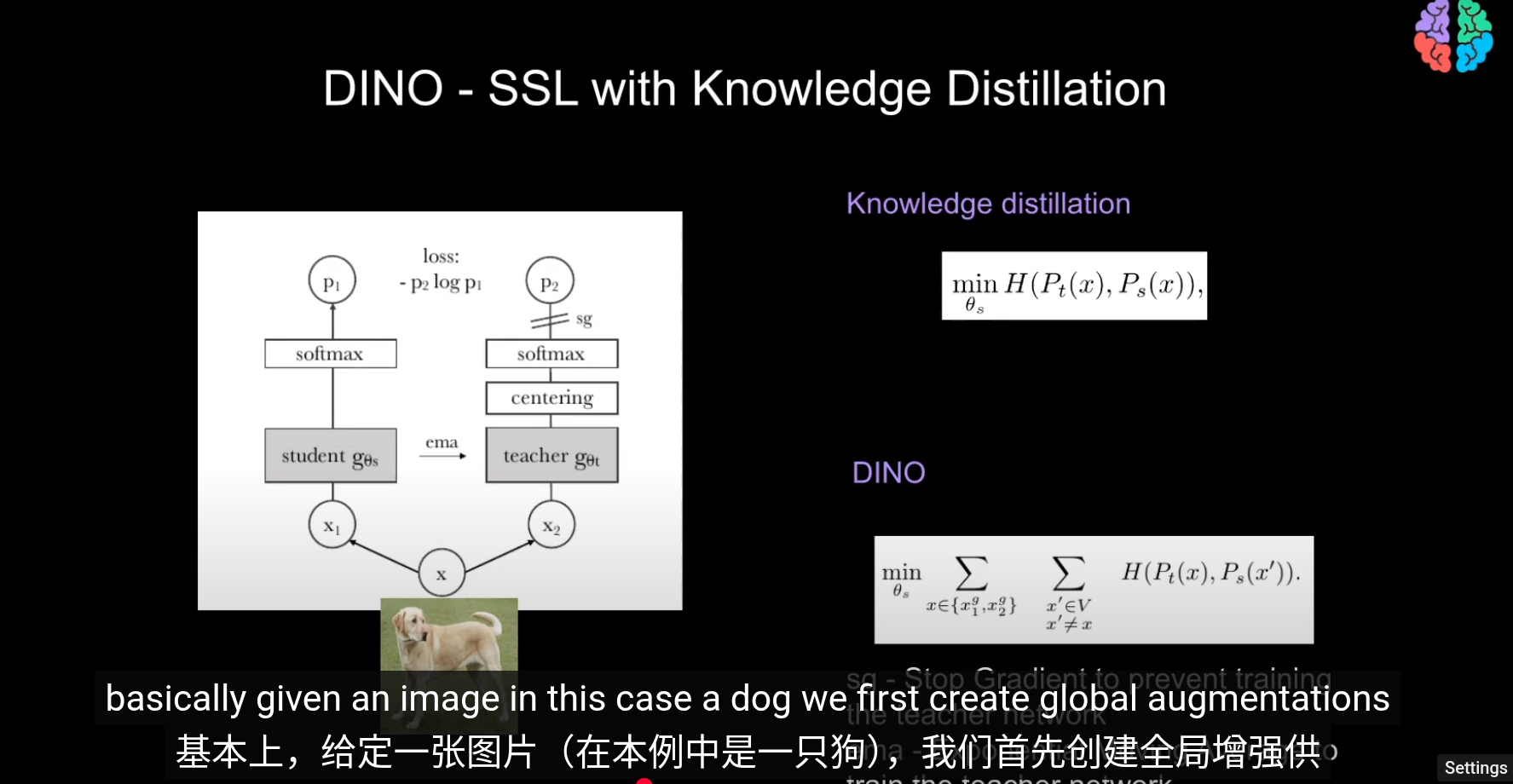
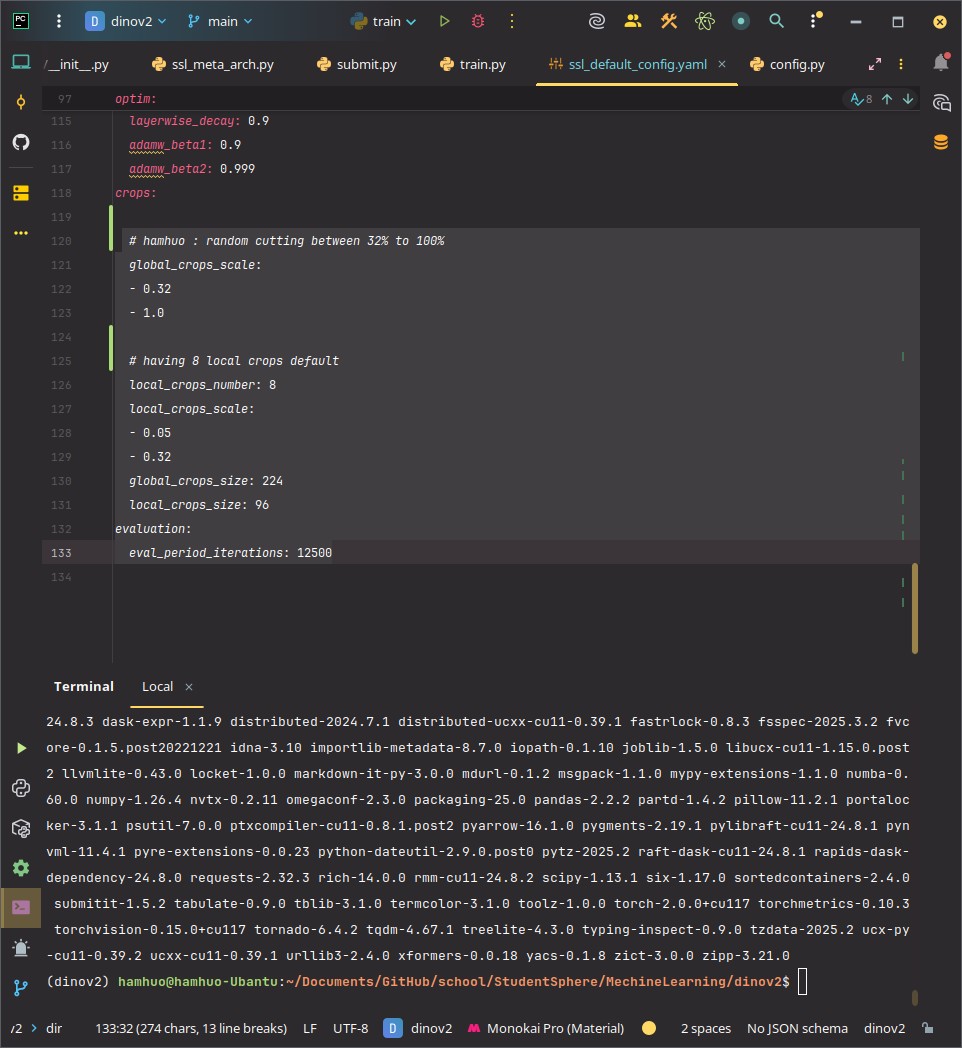
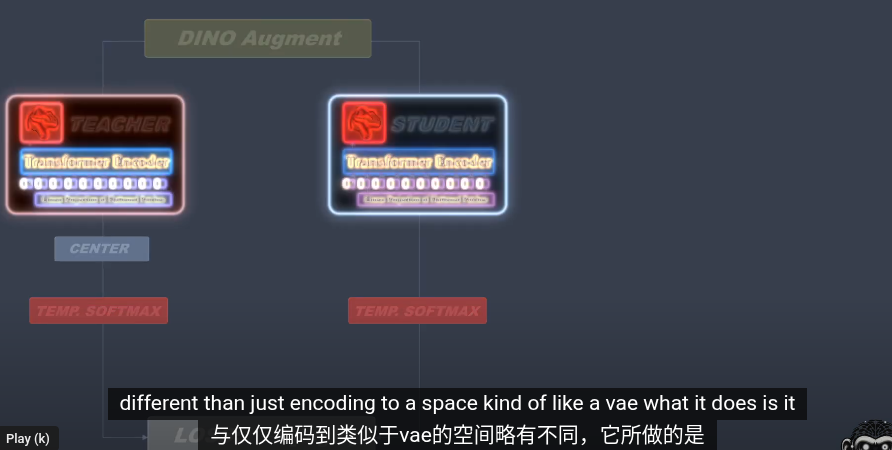
image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png

image.png image.png

image.png

image.png

image.png

image.png

image.png

image.png

之後使用softmax Tempture

image.png

image.png

DINOv2 給的溫度是0.07

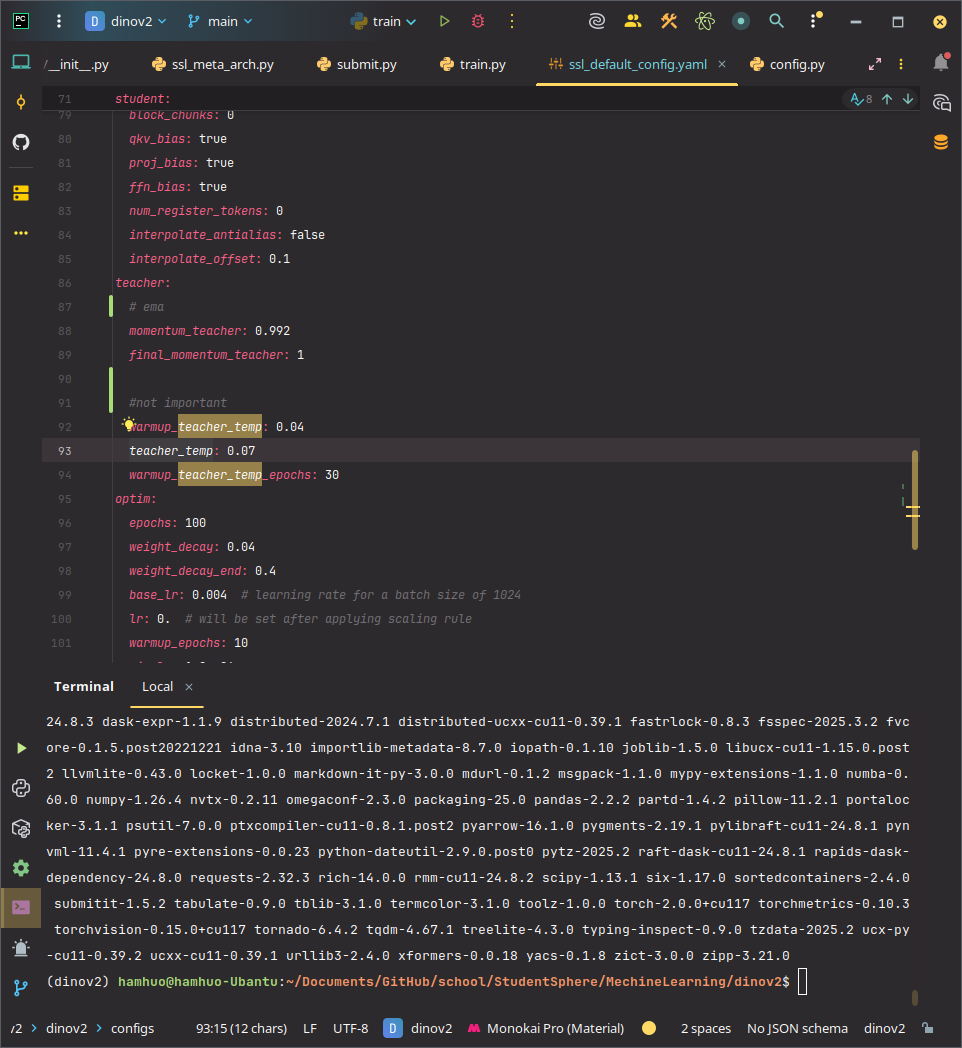
image.png

image.png

一共有65536類

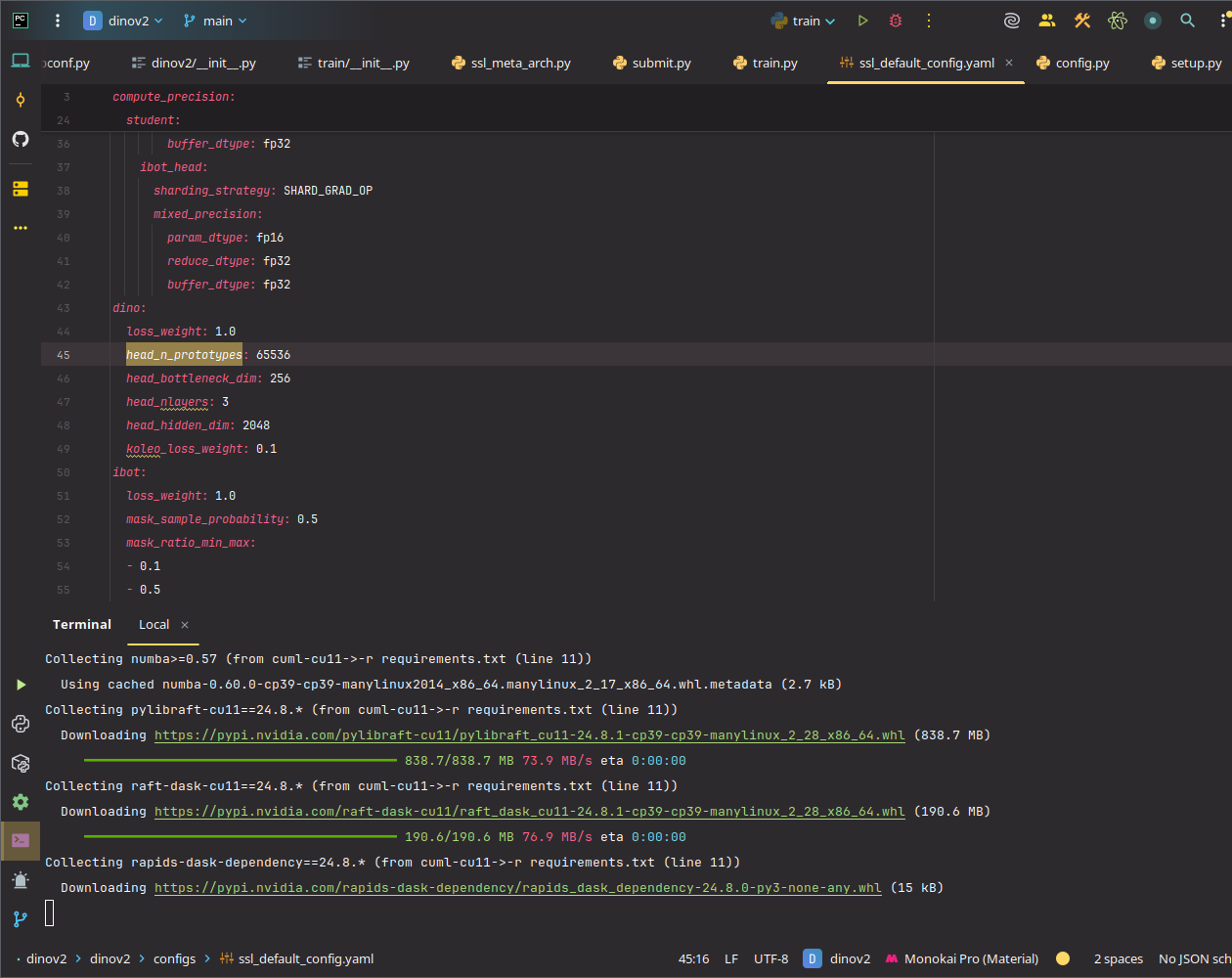
image.png

使用交叉熵來評估兩者輸出

image.png

左邊教師 右邊學生

image.png

在訓練時，同時更新教師和學生網絡是沒有意義的

image.png

image.png

image.png

image.png

image.png

DINOv2給的平滑因子是0.992

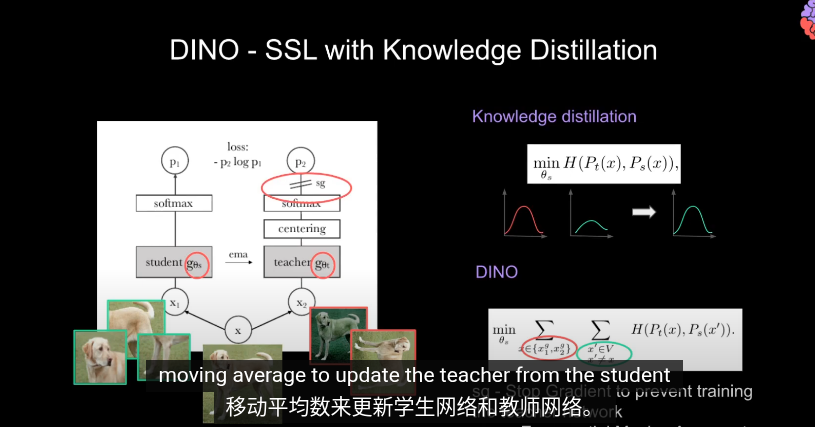
image.png

image.png

  1. EMA
  2. 數據中心化
  3. 只傳遞

image.png

image.png

我們換用

image.png

image.png

image.png

DINOV2

Introduce

想像你有一個二分類分類器，通過softmax後可以得到類別的概率

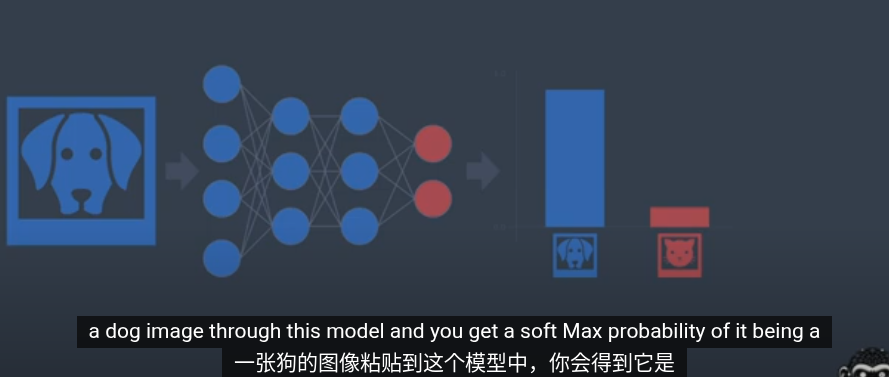
如果我們刪除分類頭

如果加上解碼器，就是VAE

我們假設這是一個3維輸入，那麼圖像會在3爲潛空間中

在latern空間中沿着某個特定方向就可以得到混合輸出

DINO使用了一種不太一樣的方法


Last modified May 6, 2025: 5/6 (d69072e)